Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 95
O cabo suporta três cargas mostradas. Determine as flechas e dos pontos e . Considere , .
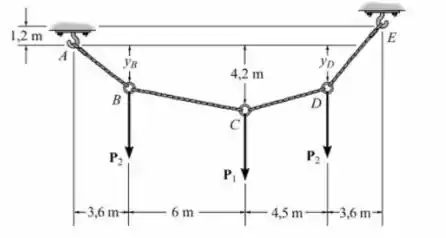
Passo 1
Fala ai galerinha, tudo beleza com vocês?
Saca só, esse problema quer que a gente encontre as flechas e .
Vamos começar calculando a soma das forças em :
No eixo também:
Somando as duas equações e simplificando:
Passo 2
Vamos analisar a junta :
No eixo fica:
Com essas duas equações, podemos obter:
E
A ultima junta que vamos analisar é a :
No eixo fica:
Com essas forças da junta , obtemos:
Passo 3
Agora, combinando o sistema:
Obtemos:
E o sistema:
Conseguimos então:
Passo 4
Por fim, basta resolvermos o sistema:
E encontramos a resposta:
Resposta
Exercícios de Livros Relacionados
39. Determine as componentes x ,y e z da carga interna na barra no ponto E . Considere F = 7 i - 12 j - 5 kk N .
Resolva o Problema 7.28 assumindo que cada viga tem peso uniforme de 3k N / m .
Determine as componentes x , y e z da carga interna no ponto C da tubulação. Despreze o peso da tubulação. Faça F 1 = - 24 i - 10 kk N , F 2 = - 80 ik N e M = - 30 kk N ∙ m .
A lança do guindaste suporta uma carga de 3,75k N através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto D da lança quando o carri
O macaco A B é usado para acertar a viga fletida D E usando a montagem mostrada. Se a força compressiva axial no macaco é de 25k N , determine o momento interno desenvolvido no ponto C da viga superio