Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 57

Para a viga do Problema 7.47, determine (a) a razão k = P / w a para a qual o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor corresponde |M|max. (Ver dica do Problema 7.55.)

Figura P7.47

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiro vamos considerar a reação w g, como a força distribuída que o solo faz na viga.

De acordo com o enunciado podemos escrever P = k w a .

Passo 2

Monte o diagrama de corpo livre da viga:

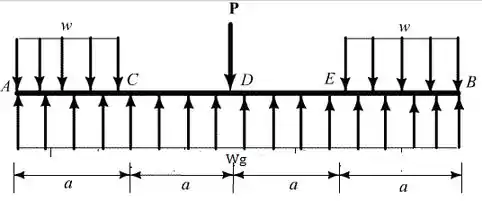
Passo 3

Aplicando o equilíbrio de forças na direção y, temos:

+ ↑ ∑ F y = 0

w g 4 a - 2 w a - P = 0

w g 4 a - 2 w a - k w a = 0

w g = w 4 ( 2 + K )

Assumindo:

w g w = α .......................................(Eq. 1)

então podemos escrever:

α =   2 + k 4

dessa forma :

k = 4 α - 2 .......................................(Eq. 2)

Como foi visto no Problema 7.47, o momento fletor interno assume valor zero no ponto A e assume valores negativos ao longo da viga, sendo que o valor M m i n ocorre na região CD. Desssa forma, para M assumir valores negativos, temos que:

w g < w

Analisando apenas a porção CD, a uma distancia x do ponto A, temos:

+ ↺ ∑ M j = 0

M + w a x - a 2 - α w x x 2 = 0

M = 1 2 w ( α x 2 - 2 a x + a 2 ) ......................................(Eq. 3)

A Eq. 3 representa a equação da curva do momento fletor interno na região CD. Para valores mínimos de M, devemos aplicar a condição d M d x = 0 . Aplicando a condição e resolvendo, temos:

w α x - w a = 0

α x - a = 0

Dessa forma, a posição ao longo da viga x m i n em que ocorre M m i n é:

x m i n = a α .....................................(Eq. 4)

Passo 4

Substitua o valor x m i n na Eq. 3 e resolva.

M m i n = 1 2 w α a α 2 - 2 a a α + 1

M m i n = 1 2 w a 2 1 α - 2 α + 1

M m i n = - w a 2 1 - α 2 α ......................................(Eq. 5)

Passo 5

O valor máximo do momento fletor ocorre no ponto D.

+ ↺ ∑ M D = 0

M D + w a 3 a 2 - 2 α w a a = 0

M m a x = M D = w a 2 2 α - 3 2 .................................(Eq. 6)

Passo 6

Seguindo a recomendação do enunciado da questão, igualamos - M m i n e M m a x e resolvemos.

w a 2 1 - α 2 α = w a 2 2 α - 3 2

4 α 2 - 2 α - 1 = 0

α = 2 ± 2 2 - 4 4 - 1 2 ( 4 )

α = 2 ± 2 5 8

α = 1 ± 5 4

α = 1 + 5 4

α = 0,809

Substituindo o valor de α na Eq. 2 e resolvendo, temos:

k = 4 0,809 - 2

k = 1,236 ...........................(resposta a)

Dessa forma, para k = 1,236 , temos o menor valor absoluto de momento fletor na viga.

Passo 7

Substitua o valor de α na Eq. 6 e resolva.

M m a x = w a 2 2 ( 0,809 ) - 3 2  

| M | m a x = 0,1180 w a 2                       ...........................(resposta b)

Resposta

  1. O valor de k, para o menor valor absoluto de momento fletor na viga é:

    2. k = 1,236

  2. O valor de | M | m a x na viga é:

| M | m a x = 0,1180 w a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois cabos de igual bitola são presos a uma torre de transmissão em B . Como a torre é estreita, o componente horizontal da resultante das forças exercidas pelos cabos em B deve ser nulo. Sabendo que
O vão central da ponte Verrazano-Narrows consiste em dois tabuleiros uniformes suspensos por quatro cabos. O projeto da ponte levou em conta o efeito de mudanças extremas de temperatura, que fazem a f
Cada cabo dos vãos laterais da ponte Golden Gate sustenta uma carga w = 153k N / m ao longo da horizontal. Sabendo que para os vãos laterais a distância vertical máxima h de cada cabo até a corda A B
Um cano de vapor pesando 675k N que passa entre dois prédios, distanciados 12m entre si, é sustentado por um sistema de cabos tal como mostra a figura. Considerando que o peso do cabo é equivalente a
O cabo A B sustenta uma carga uniformemente distribuida ao longo da horizontal, como mostra a figura. Sabendo que o ponto mais baixo do cabo é localizado a uma distância a = 0,6m abaixo de A , determi