Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 55
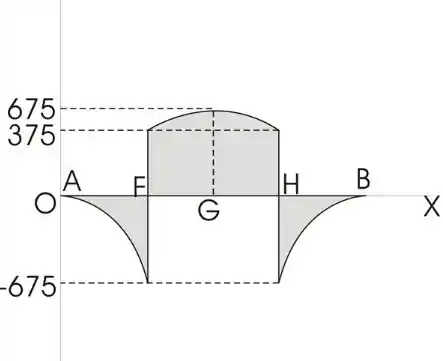
Para o elemento estrutural do Problema determine o ângulo para o qual o valor absoluto máximo do momento fletor na viga é o menor possível, o valor correspondente de . (Dica: trace o diagrama de momento fletor e depois iguale os valores absolutos dos maiores momentos fletores positivo e negativo obtidos.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
De posse do valor , temos que:
Passo 2
Colocando , na equação, . Você encontrará:
Então para os valores a direita de :
E:
Passo 3
Analisando o diagrama do momento, você obterá o valor absoluto máximo do momento:
Resposta
Exercícios de Livros Relacionados
Um cabo tem massa por unidade de comprimento de 0,65k g / m e é suspenso em dois isoladores de igual elevação separados a uma distância de 120m entre si. Se a flecha do cabo é 30m entre si. Se a flech
Um comprimento de 50,5m do arame tendo a massa por unidade de comprimento de 0,75k g / m é usado em um vão de 50m . Determine (a) a flecha aproximada do arame, (b) a tensão máxima no arame. [Dica: Use
O cabo A B de vão L e uma viga simplesmente apoiada A ' B ' de mesmo vão estão sujeitos a carregamentos verticais idênticos, como mostra a figura. Mostre que a intensidade do momento fletor no ponto C
Um fio de 90m de comprimento está suspenso por dois pontos de igual elevação, que estão afastados 60m entre si. Sabendo que a tração máxima é 300N , determine (a) a flecha do fio e (b) a massa total d
Um cabo para teleférico de 200m de comprimento e massa por unidade de comprimento de 3,5k g / m é suspenso entre dois pontos de igual elevação. Sabendo que a flecha é 50m , determine (a) a distância h