Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 107
Um cabo tem massa por unidade de comprimento de e é suspenso em dois isoladores de igual elevação separados a uma distância de entre si. Se a flecha do cabo é entre si. Se a flecha do cabo é , determine (a) o comprimento total do cabo, (b) a tração máxima no cabo.
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar nossa vida, fica mais ou menos assim:
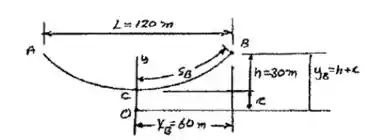
Então, a gente consegue encontrar:
Resolvendo por tentativa e erro, achamos:
Passo 2
Show de bola, agora vamos calcular , é praticamente da mesma forma:
E o comprimento do cabo é:
Passo 3
Por fim, a gente só precisa calcular a tração máxima no cabo, bora lá:
Resposta
Exercícios de Livros Relacionados
Uma corda uniforme de 1250m m de comprimento passa por uma roldana em B e é fixada em um pino de apoio em A . Sabendo que L = 500m m e desprezando o efeito do atrito, determine o menor dos dois valore
À esquerda do ponto B , o cabo longo A B D E repousa sobre a superfície horizontal áspera mostrada na figura. Sabendo que a massa por unidade de comprimento do cabo é 2k g / m , determine a força F qu
Foi determinado experimentalmente que o momento fletor no ponto K da estrutura mostrada na figura é 300N ⋅ m , Determine (a) a tração nas hastes A E e F D , (b) a força in
O cabo A C B tem massa por unidade de comprimento de 0,45k g / m . Sabendo que o ponto mais baixo do cabo está localizado a uma distância a = 0,6m abaixo do apoio A , determine (a) a localização do po
Um cabo tem massa por unidade de comprimento de 3k g / m e é erguido tal como mostra a figura. Sabendo que L é 6m , determine os dois valores da flecha h para os quais a tração máxima é 350N .