Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 116
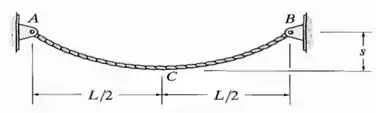
O cabo tem peso específico e área de seção transversal . Se a flecha for pequena, de modo que o comprimento do cabo seja aproximadamente e seu peso possa ser distribuído uniformemente ao longo do eixo horizontal, determine a tensão normal média no cabo em seu ponto mais baixo .
Passo 1
Fala! Desejamos encontrar a tensão normal média no cabo dado que seu peso pode ser distribuído uniformemente ao longo do eixo horizontal. Para achar a tensão a gente usa a fórmula da tensão média:
Mas precisamos achar . Vira uma questão de achar esforços internos na seção de .
Nesse tipo de questão, o bizu é a gente cortar a nossa peça nessa seção e olhar só para o lado dela que a gente já tem todas as informações das forças atuando), posicionar as componentes dos esforços internos nela, achar eles pelas equações de equilíbrio.
Por simetria, as reações precisam ser a metade do peso da corda completa. Então:
Como a gente pode aproximar o comprimento dele por :
Vamos fazer o corte e escolher o lado esquerdo:
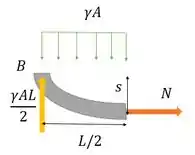
Onde é o peso por comprimento , uma carga distrubuída. Vamos seguir!
Passo 2
Dessa forma, pela equação de equilíbrio vamos ter
Adotando o sentido anti-horário como positivo
Sendo assim, nossa tensão normal média será dada por