Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 8
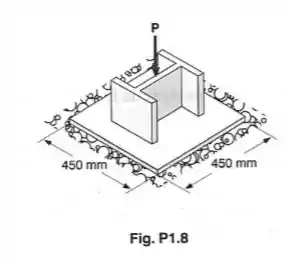
Uma carga axial é suportada por uma pequena coluna , de seção transversal igual a e é transmitida a uma fundação de concreto por uma placa quadrada de , como mostrado. Sabendo-se que a tensão normal média na coluna não poderá exceder , e que a tensão de esmagamento média sobre a fundção de concreto não poderá exceder , determine a máxima carga admissível.
Passo 1
Neste problema o enunciado nos fornece dois limites:
- Tensão normal máxima da coluna deve ser inferior a .
- Tensão de esmagamento máxima da fundação deve ser inferior a
Então vamos ter de calcular ambas as tensões e ver aonde está a nossa limitação.
Passo 2
Vamos calcular a tensão normal máxima da coluna.
Onde é a tensão máxima de , é a força que queremos achar a a área da coluna, que foi fornecida e é igual a . Portanto, substituindo na equação temos:
Passo 3
Agora iremos fazer algo análogo para a tensão de esmagamento da fundação.
Onde é a tensão de esmagamento máxima e vale , é a força que queremos achar e é a área do quadrado de .
Passo 4
Então veja que a gente achou dois valores para :
Para que ambos os critérios de tensão máxima sejam satisfeitos então devemos utilizar a menor força dentre as duas. Logo, a nossa resposta é: