Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 6
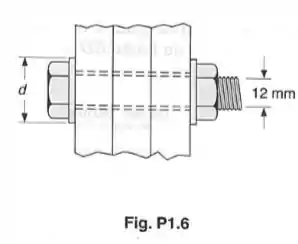
Três pranchas de madeira são unidas por uma série de parafusos, formando uma coluna. O diâmetro de cada parafuso é de 12 mm, e o diâmetro interno de cada arruela é de 15 mm, que é ligeiramente maior que os furos das pranchas. Sabendo-se que o diâmetro externo de cada arruela é de , e que a tensão de esmagamento média entre as arruelas e as pranchas não deve exceder a , determine a máxima tensão normal admissível em cada parafuso.
Passo 1
Neste exercício o parafuso é utilizado para fixar as três pranchas por meio de uma força axial, vamos chamar essa força de e é demonstrada na figura abaixo:
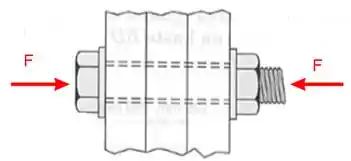
Essa força axial sujeita a arruela, as pranchas e o parafuso à uma tensão normal . Apesar da forças ser a mesma para todos os componentes, a tensão normal é diferente pois as áreas são distintas. Lembre-se que:
O problema pede a tensão máxima admissível no parafuso e nos fornece o dado de que a tensão de esmagamento das arruelas não deve ultrapassar .
Então vamos resolver o problema da seguinte forma: A partir do limite da tensão de esmagamento (em conjunto com a área da arruela) vamos descobrir a força . Com a força e a área do parafuso vamos achar a tensão máxima que o problema pede. Então vamos lá!
Passo 2
Vamos descobrir a força que faz uma tensão de esmagamento de na arruela.
Então vamos achar a área da arruela, como mostrada abaixo:
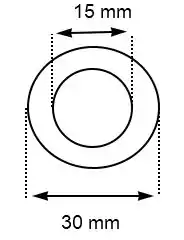
A área vai ser dada pela área do círculo maior menos a área do círculo menor.
Agora vamos substituir na equação da tensão de esmagamento
Passo 3
Com a força o problema fica mole mole. Para achar a tensão normal no parafuso basta substituir em
Calculando a área do parafuso
Logo,