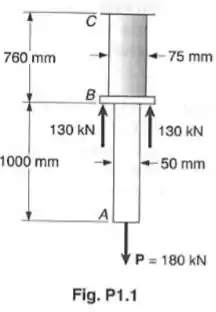
Duas barras cilíndricas maciças são soldadas no ponto B como indicado. Determine a tensão normal no ponto médio de cada barra.
Passo 1
Primeiro devemos observar que as duas barras mencionadas são as barras CB (grossa e escura) e a barra BA (fina e clara).
O problema pediu para calcular a tensão normal , que é dada por
Onde é a força interna que atua na barra e a área da seção transversal.
Obs: Galera, o livro do Beer utiliza a letra na fórmula como a força interna que atua na barra. Além disso, em alguns problemas o livro também utiliza a letra como uma força externa qualquer (que não é necessariamente a força que atua no interior da barra, embora nesse problema seja; acredito que o autor tenha feito isso para facilitar a compreensão, mas é importante perceber que as duas são distintas). De qualquer forma irei me ater à nomenclatura do autor.
Então veja que as informações importantes para a resolução do problema são:
- As forças;
- Os diâmetros (para calcular a área).
O comprimento das barras é inútil para esse exercício ;)
Passo 2
Já existem três forças, duas de para cima e uma de para baixo. Como é maior do que então existe uma força externa , que equilibra o sistema e ainda desconhecemos. Então vamos achar essa força.
O único lugar que essa força pode atuar de modo a ser uma força externa, e assim equilibrar o sistema, é no ponto . Logo, vamos aplicar essa força no ponto :
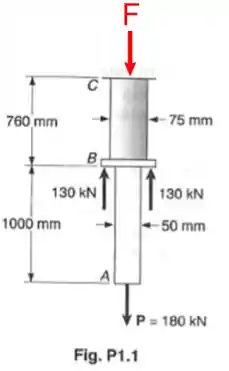
Repare que aqui a força foi colocada de cima para baixo por uma questão de conveniência, porque a gente sabe que para equilibrar a barra a força deve ser apontada para baixo. Mas o sentido dessa força não importa, é pura convenção!! Caso o sentido esteja certo acharemos um valor positivo, caso esteja errado acharemos um valor negativo o que significa que o sentido deve ser trocado.
Como só temos forças na vertical vamos ter que o somatório das forças em é igual a zero:
Vamos considerar o sentido positivo para cima, logo teremos:
Passo 3
Afim de calcular a tensão normal vamos, então, calcular a área e a força atuante. Vamos fazer isso primeiro para a barra BC.
A área é mais fácil de ser calculada e vem diretamente do diâmetro fornecido que é de 75 mm. Podemos calcular a área de dois jeitos, o primeiro:
E o segundo:
Isso porque o diâmetro é o dobro do raio
Como o problema nos forneceu o diâmetro então vamos utilizar o primeiro jeito mesmo:
Ou
Passo 4
Agora vamos aplicar a equação da tensão normal:
Mas temos várias forças então quem é essa força ?
A força é a força que atua dentro da barra, então a gente tem que fazer um corte na barra BC e ver que força é essa.
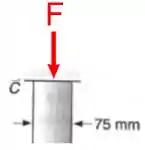
Olha o corte que bonitinho!
Mas essa força não atua “dentro” da barra, então vamos ter algo mais ou menos assim:
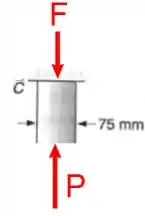
Agora sim! A força que a gente realmente quer é a que atua bem no corte! E não precisa de muito para ver que (em módulo pelo menos né), além disso fica bem nítido que a barra está sob efeito de compressão (olha como e “amassam” a barra).
Daí temos que
Passo 5
Então agora sim é só colocar na fórmula
Aqui vai um truque que eu uso, mas podem ficar à vontade para resolver da forma que preferirem. Eu gosto de utilizar a força em Newton e a área em milímetro quadrado porque aí a tensão já dá direito em . Olha só!
Passo 6
Agora iremos fazer os mesmo procedimentos para a barra AB. Primeiro vamos calcular a força atutante dentro da barra AB. Para isso, vamos observar o desenho novamente:
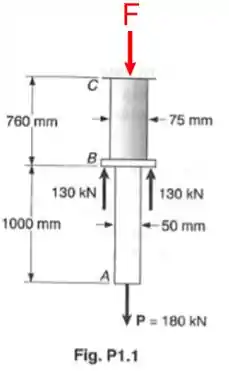
Nós já sabemos que a força vale , mas, para resolver a barra AB, nem precisamos de na verdade, porque a força interna em AB é a própria força de .
Mas como assim?
Só olhar como fica o corte da seção AB:
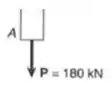
Para manter o equilíbrio temos que ter uma força interna igual a para contrabalancear.
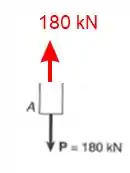
Passo 7
Vamos calcular a área da barra AB:
Passo 8
Substituir na equação da tensão normal:
Resposta
Barra BC:
Barra AB: