Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 103
Determine o valor máximo do momento fletor de modo que a tensão de flexão no elemento não ultrapasse
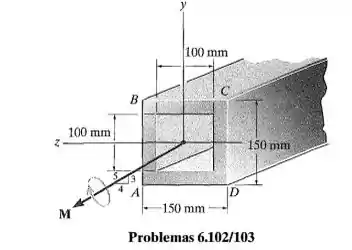
Passo 1
Primeiro, vamos decompor o momento:
O momento de inércia será:
Passo 2
Com a tensão, podemos determinar o momento:
Portanto, o momento será:
Resposta
Exercícios de Livros Relacionados
Resolver o prob. 4.188 considerando que o anel tem um raio interno r 1 = 15m m e uma seção circular de diâmetro d = 20m m
Três placas são soldadas juntas, para formar a viga curva mostrada. Para M = 1130N m , determinar a tensão no (a) ponto A; (b) ponto B; (c) centroide da seção transversal.
Uma conexão de aço tem a seção transversal mostrada e os furos estão dispostos segundo o ângulo central β . Determinar (a) O maior valor admissível para β para que não ocorram tensões de compressão, n
Usando a equação 4.66, desenvolva a expressão para R, da figura abaixo, para uma seção transversal circular.
Usando a equação 4.66, desenvolva a expressão para R, da figura abaixo, para uma seção transversal trapezoidal.