Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 58
Cada uma das barras da treliça tem área de seção transversal de 780mm². Determine a tensão normal média em cada elemento resultante da aplicação da carga P = 40 kN. Indique se a tensão é de tração ou de compressão.
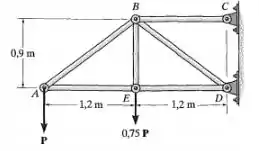
Passo 1
Primeiramente, devemos calcular as forças em cada barra. Para isso, vamos utilizar as equações da estática e as forças decompostas nas direções x e y para achar as reações em cada pino (isso é chamado método dos nós).
Mas antes vamos mostrar onde estão as forças de reação.
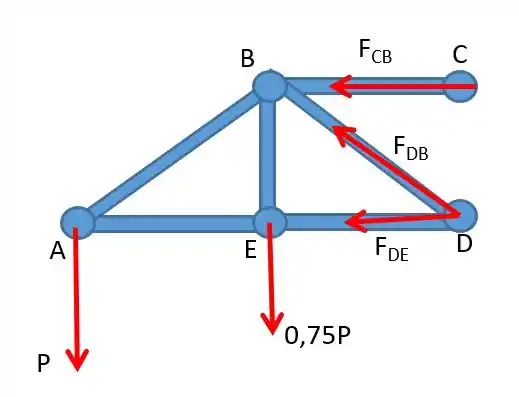
Olha como todas as forças seguem suas respectivas barras, vamos fazer isso para todas as outras barras também.
Passo 2
Vamos começar pelo ponto , por quê? Porque a gente que escolhe, bebê, além disso nesse ponto existem duas forças desconhecidas, logo quando aplicarmos o momento nele vamos sumir com duas incógnitas!
No ponto D, tomando o sentido anti-horário como positivo:
Passo 3
Como estamos aplicando o métodos dos nós temos que analisar nó a nó, lembrando que as forças sempre vão apontar de dentro para fora do nó (nos últimos passos vamos entender o porque disso, por enquanto só confia). Então vai ficar assim:
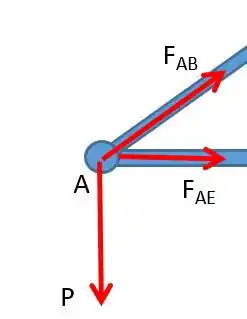
Olhem como estamos pegando apenas a componente vertical da força, logo vamos ter que decompô-la utilizando o seno do ângulo EÂB, ou seja:
Retomando:
Agora para o eixo horizontal:
Assim como calculamos a componente vertical, vamos utilizar agora o cosseno para calcular a horizontal:
Retomando
Passo 4
Para o ponto E:
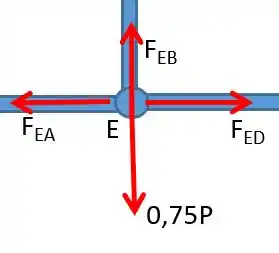
Para o eixo vertical:
Passo 5
Vamos fazer a mesma coisa para o ponto :
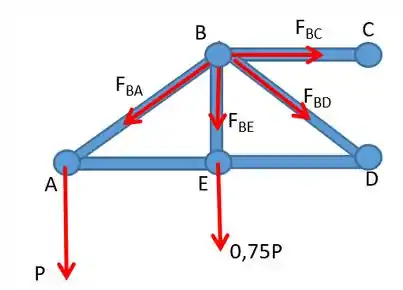
Pegando as forças verticais.
Perceba que os termos análogos, como e são iguais porque atuam na mesma barra! Aplicamos o princípio da ação e reação!! Assim, não precisamos ficar calculando tudo de novo!
Além disso é válido lembrar que o ângulo que atua em é igual ao ângulo de por isso em ambos os termos aparece o 0,6; como mostrado abaixo:
Passo 6
Agora vamos calcular a tensão, que é basicamente dividir a força atuante na barra pela sua área:
obs: Aqui vai uma diquinha! Se a área já é dada em a gente pode deixar com essa unidade e (utilizando também a força em ) vamos ter um resultado em . Porque , como está no denominador a potência fica positiva.
Como já temos a área da barra e calculamos as forças em cada barra, podemos calcular as tensões em cada barra:
Ah mas como você sabe que é tração ou compressão?
É só ver se a força é positiva (tração) ou negativa (compressão). Por isso em problemas como este duas coisas são MUITO IMPORTANTE:
- Colocar sempre as forças partindo dos nós em direção à barra (como foi feito durante todo o problema).
- se um valor der negativo, “levar” ele até o final. Não pode alterar de jeito nenhum.