Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 103
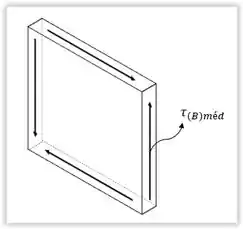
O tubo é feito de plástico, tem de espessura, e as dimensões médias mostradas na figura. Determine a tensão de cisalhamento média nos pontos e se ele for submetido ao torque . Mostre a tensão de cisalhamento nos elementos de volume localizados nesses pontos.
Passo 1
Oi pessoal, tudo bom com vocês?
A questão pede que determinemos a tensão de cisalhamento média nos pontos e , e que façamos um desenho dessas tensões no elemento de volume em cada um dos pontos.
Dados fornecidos:
Vamos incialmente determinar a área média (). Essa é a área que o contorno da linha central da espessura do tubo forma. Para melhor visualização analisaremos a imagem:
Como podemos observar essa área é formada por um retângulo e um triângulo, logo sua área é:
Passo 2
Agora iremos determinar as tensões que ocorrem nos pontos e . Como podemos notar, a espessura e a área média é a mesma nesses dois pontos, por isso teremos:
Com isso teremos:
Passo 3
Vamos então ao desenho dessas tensões de cisalhamento médias.
Primeiro determinaremos a localização de uma tensão de cisalhamento no elemento de volume. As outras são reações a esta para manter o corpo em equilíbrio.
Essa primeira tensão é a tensão gerada pelo torque . Como o torque é no sentido anti-horário, a tensão gerada por ele no ponto será orientada para cima e no ponto estará para esquerda.
Sendo assim, as outras tensões serão reações provocadas por esta, a fim de manter o corpo em equilíbrio. Com isso teremos:
Ponto :
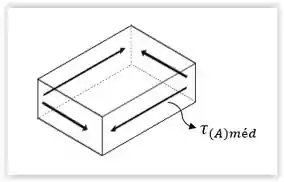
Ponto :
