Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 59
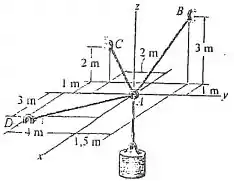
Se cada cabo pode suportar uma tração máxima de , determine a maior massa que o cilindro pode ter para o equilíbrio.
Passo 1
Fala! Ele quer o valor máximo de do cilindro sabendo que a maior força de tração não pode ultrapassar . A estratégia aqui é achar as trações em função de , e descobrir quem é a maior. A partir dela e do valor máximo , achamos .
O que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
Logo, fazendo o diagrama de corpo livre tem-se:
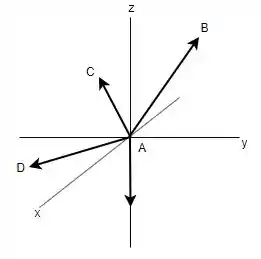
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Em seguida, o equilíbrio de forças deve ser analisado nas três dimensões , pelo fato de as forças estarem atuando em todos esses três sentidos.
Como a geometria do problema é mais complexa, é mais jogo a gente escrever as forças na forma vetorial. Fazer a soma vetorial, e igualar cada componente dessa soma a zero, já que estamos no equilíbrio, bele? Vamos!
Passo 2
Tem-se que o cilindro exerce uma força peso para baixo que tem intensidade de . De forma vetorial nós temos:
Também é possível denotar as forças , e na forma vetorial. O que a gente precisa fazer é achar um vetor unitário na direção e sentido da força, e multiplicar a intensidade da nossa força por ele.
Percebe que para a AB, um vetor no sentido da força seria o que sai de A e vai para B. Podemos acha-lo pela diferença entre essas coordenadas desses pontos. Fazendo final menos inicial:
Aí para achar o vetor unitário só dividir esse cara pelo módulo dele. Nossa força em forma vetorial fica:
Fazemos o mesmo para as outras forças. Aqui nosso vetor sai de A e vai para C:
E para :
Passo 3
O equilíbrio requer quer o somatório de forças em cada dimensão seja nulo, ou seja:
Olhando para cada eixo, vamos igualar a soma em cada componente a zero.
Por fim para :
Passo 4
A partir das equações (1) e (2) é possível obter relações entre as forças.
Vamos usar essas equações dessa forma:
Logo
Como e são frações de , temos que a maior força é . Ela vai ser a tração máxima. Como a tração máxima permitida em cada cabo é de , então .
Passo 5
Logo, com esse valor das forças e a equação (3), é possível determinar a maior massa do cilindro:
Logo,
Obs: ficamos diferente do gabarito, mas tamos certinhos, tá?