Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 64

A viga uniforme tem massa de por metro de comprimento. Determine a tensão nos dois cabos de suporte e a reação em .

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar as tensões nos cabos e e a reação no apoio em . Vamos analisar apenas a viga com o seu peso atuando no centro de gravidade (na metade do comprimento), as tensões no ponto e a reação do apoio em . O peso da viga de e massa pode ser obtido por:

O centro de gravidade está na metade do comprimento da vida, ou seja, à direita do ponto .

Uma vez que os cabos são simétricos, podemos deduzir que suas componentes horizontais (direção ) vão se anular e, como restarão apenas forças verticais (direção ), a reação de apoio em será vertical também. Para facilitar nossos cálculos, vamos considerar que o ponto será o centro do sistema de coordenadas por onde os eixos , e se interceptam.

A partir dessas considerações, podemos fazer o equilíbrio de momentos em torno do eixo . Como as tensões dos cabos estão aplicadas no ponto onde o eixo passa, elas não produzem momento em torno desse ponto, assim nossa única incógnita é a reação .

Passo 2

Show, feito isso, para determinar as tensões precisamos primeiro descobrir o ângulo que os cabos formam com a vertical.

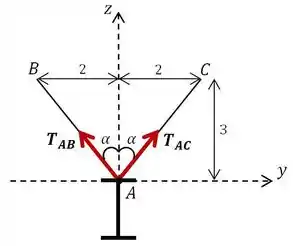
Com isso, podemos usar equilíbrio de forças nas direções e para descobrir e . Lembrando que precisamos incluir e que estão atuando verticalmente ao longo da viga. Começando pelo eixo :