Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 61
Cada um dos cilindros tem uma massa de . Se os coeficientes de atrito estático nos pontos de contato são , , e , determie o menor momento de binário necessário para girar o cilindro .
Passo 1
O problema pede que descubra o menor momento de binário para começar o giro, então, para vencer o atrito.
Bom galera, pra facilitar a gente começa fazendo um diagrama de corpo livre de um dos corpos primeiro e depois o outro pra analisar as forças, mas antes nota que a gente não tem a força peso e sim a massa, a gente resolve isso:
Assim, o diagrama de corpo livre começando pelo cilindro que tem menos forças atuantes:
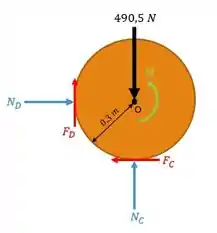
Passo 2
Bom, agora percebe que só tem duas forças que atuam no eixo , então elas devem ser iguais e sentidos opostos para o corpo ficam em equilibrio:
E a gente sabe que a força de atrito calcula-se por , então:
Que também é:
Então analisando o eixo agora:
Substituindo a força de atrito e o que já tinhamos encontrado:
Então com a mágica da matemática a gente já tem tudo que precisa pra calcular todas as forças atuantes nesse cilindro, inclusive o momento, sem nem precisar do outro cilindro.
Passo 3
Beleza, agora a gente encontra as duas forças de atrito que agem no cilindro, porque só elas geram momento em , concorda comigo?
Show de bola, a gente vai calcular com o que a gente já tem:
Lembra que também podemos calcular o atrito com a normal, desse jeito:
Passo 4
Calma, só falta mesmo calcular o momento agora, sabendo que o corpo tá em equilibrio a soma dos momentos tem que dar nula, então: