Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 133
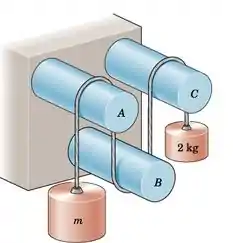
Determine a faixa de massa m sobre a qual o sistema está em equilíbrio (a) se o coeficiente de atrito estático for 0,20 em todos os três eixos fixos e (b) se o coeficiente de atrito estático associado ao eixo B for aumentado para 0,50.
Passo 1
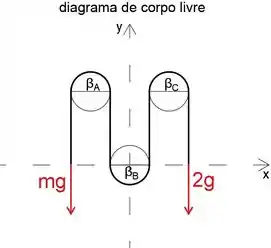
Uma vez que temos três eixos, podemos escrever a expressão para a relação entre as tensões T1 e T2 como
Podemos ver a partir do desenho que todos os ângulos de contato são os mesmos
Portanto, podemos escrever a expressão acima como
Podemos escrever a expressão para as tensões T1 e T2
Passo 2
Observe que a tensão T2 é sempre maior que T1 e para aumentar a força do cilindro de 2 kg mg deve ser maior que o peso 2g, portanto
Como a força mg é maior que o peso 2g, colocaremos os valores de T1, T2, na expressão (2) para determinar a força mg necessária para elevar o cilindro
Podemos dividir os dois lados da equação por g
Para diminuir a força do cilindro, mg deve ser menor que 2g de peso, portanto
Como a força mg é menor que o peso 2g, colocaremos os valores de T1, T2 na expressão (1) para determinar a força mg necessária para elevar o cilindro
Passo 3
Podemos dividir os dois lados da equação por g
Uma vez que escrevemos a expressão para a massa m necessária para diminuir e aumentar o cilindro de 2 kg, podemos dizer que o sistema está em equilíbrio para o intervalo de
Passo 4
(a)
Tudo o que temos que saber é substituir , e por 0,20 na expressão (3)
(b)
Agora vamos substituir e por 0,20 e por 0,50 na expressão (3)