Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 129

O torno de 4600 lb com centro de massa em G é posicionado com o auxílio da cunha 5 ° de aço. Determine a força horizontal P necessária para remover a cunha se o coeficiente de atrito para todas as superfícies de contato for 0,30. Mostre também que nenhum movimento horizontal do torno ocorre.

Passo 1

Primeiro, vamos desenhar o diagrama de corpo livre do torno

Vamos assumir que o movimento horizontal é impedido

Observe que vamos desprezar a altura da cunha de aço

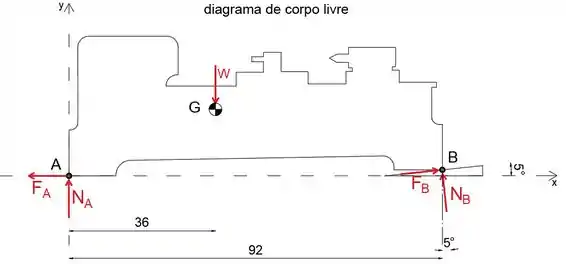
Passo 2

Equacionando a soma dos momentos sobre o ponto A a zero, determinaremos a força de reação normal NB

∑ M A = 0

36 W - 92 N B cos ⁡ 5 ° - 92 F B sin ⁡ 5 ° = 0

Uma vez que o coeficiente de atrito é μ = 0,30, podemos substituir FB por 0,30NB e W por seu valor

36 ∙ 4600 - 92 N B cos ⁡ 5 ° - 92 ∙ 0.30 N B sin ⁡ 5 ° = 0

165   500 - 94.06 N B = 0

N B = 165   500 94.06

N B = 1   759.52   lb

Passo 3

Agora podemos determinar a força de atrito FB

F B = 0.30 N B

F B = 0.30 ∙ 1   759.52

F B = 527.85   lb

Para verificar nossa suposição de que o movimento horizontal é evitado, precisamos determinar as forças de reação no ponto A, igualando a soma das forças na direção x e y a zero

∑ F x = 0

- F A + F B cos ⁡ 5 ° - N B sin ⁡ 5 ° = 0

F A = F B cos ⁡ 5 ° - N B sin ⁡ 5 ° = 0

F A = 527.85 cos ⁡ 5 ° - 1   759.52 sin ⁡ 5 ° = 0

F A = 372.49   lb

∑ F y = 0

N A - W + N B cos ⁡ 5 ° + F B sin ⁡ 5 ° = 0

N A = W - N B cos ⁡ 5 ° - F B sin ⁡ 5 °

N A = 4   600 - 1   759.52 cos ⁡ 5 ° - 527.85 sin ⁡ 5 °

N A = 2   801.17   lb

Passo 4

A força de atrito máxima atuando no ponto A é

F A m a x = μ N A

F A m a x = 0.30 ∙ 801.17

F A m a x = 840.35   lb

Podemos ver que a força de atrito FA é menor que a força de atrito máxima F A m a x

F A < F A m a x

O que significa que o movimento horizontal é impedido

A seguir, desenharemos o diagrama de corpo livre da cunha

Observe que assumimos que o deslizamento ocorre simultaneamente em B e C

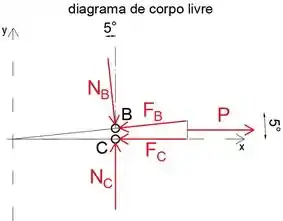
Passo 5

Ao igualar a soma das forças na direção y a zero, podemos determinar a força de reação normal NC

∑ F y = 0

N C - N B cos ⁡ 5 ° - F B sin ⁡ 5 ° = 0

N C = N B cos ⁡ 5 ° + F B sin ⁡ 5 °

N C = 1   759.52 cos ⁡ 5 ° + 527.85 sin ⁡ 5 °

N C = 1   798.83   lb

Agora podemos determinar a força de atrito FC

F C = 0.30 N C

F C = 0.30 ∙ 1   798.83

F C = 539.65   lb

Passo 6

Finalmente, ao igualar a soma das forças na direção x a zero, podemos determinar a força P

∑ F x = 0

- F C - F B cos ⁡ 5 ° + N B sin ⁡ 5 ° + P = 0

P = F C + F B cos ⁡ 5 ° - N B sin ⁡ 5 °

P = 539.65 + 527.85 cos ⁡ 5 ° - 1   759.52 sin ⁡ 5 °

P = 912.14   lb

Resposta

P = 912.14   lb

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo passa em torno de três tubos paralelos. Dois dos tubos são fixos e não podem rodar, enquanto o terceiro tubo é girado vagarosamente. Sabendo que os coeficientes de atrito são μ s = 0,25 e μ k
A velocidade de um tambor de freio mostrado na figura é controlada por uma cinta fixada a uma cinta fixada a uma barra de controle A D . A força P de intensidade de 110N é aplicada na barra de control
Um cabo passa em torno de três tubos paralelos. Sabendo que os coeficiente de atrito são μ s = 0,25 e μ k = 0,20 , determine (a) o menor peso W para o qual o equilibrio é mantido, (b) o maior peso W q
Sabendo que a = 100m m , determine o máximo valor do coeficiente de atrito estático para o qual o freio é autotravante quando o tambor roda no sentido anti-horário.
Resolva o Problema 8.116 , supondo que o tambor B esteja fixo e não possa girar.