Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 38
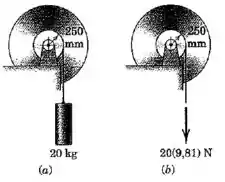
Cada um dos dois tambores e seus cubos associados com de raio possui uma massa de e um raio de giração em relação a seu centro de . Calcule a aceleração angular de cada tambor. O atrito em cada mancal é desprezível.
Passo 1
Como o sistema não está em equilíbrio, não podemos simplesmente tratar os dois casos como equivalentes, mesmo considerando que a força no item (b) é igual ao peso do cilindro no item (a). Isso vai ficar claro ao longo da resolução.
(a) Vamos supor que o tambor gire com aceleração angular , nesse caso, a aceleração linear do tambor interno, onde a corda está enrolada é:
E então a segunda lei de Newton aplicada ao cilindro fica da seguinte forma:
Temos uma equação com duas variáveis, para poder encontrá-las precisamos de uma segunda equação.
Passo 2
Vamos encontrar essa segunda equação usando uma equação de momentos, ainda pensando no sistema do item (a):
E a única força que gera momento em torno do ponto é a tração do fio, que está a do centro:
E o momento de inércia em relação ao ponto é
Então ficamos com um sistema de duas equações:
Que pode ser resolvido para determinar :
Passo 3
(b) No caso do item , podemos usar apenas uma equação de momentos:
E o único momento é o da força de , e o momento de inércia ainda é , então:
Resposta
(a) .
(b).