Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 81
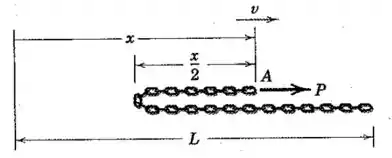
Uma corrente de elos de comprimento com uma massa de repousa sobre uma superfície horizontal lisa quando a extremidade volta sobre si mesma puxada por uma força aplicada à extremidade . (a) Calcule o valor necessário de para fornecer a uma velocidade constante de . (b) Calcule a aceleração da extremidade se e se quando
Passo 1
Podemos pensar na “metade superior” da corrente como se fosse um sistema cuja massa está aumentando, Isso vai simplificar bastante as nossas contas.
Nesse caso, é a única força externa agindo sobre o sistemas, então:
Nosso primeiro objetivo é calcular a força no caso em que se move com uma velocidade constante.
Passo 2
(a) Bom, já que é uma constante:
E nossa equação fica:
Como todas as partes da corrente se movem com a mesma velocidade, temos:
E agora vamos procurar uma expressão para a taxa de variação da massa . Estamos considerando apenas a quandidade de massa que está no trecho de comprimento , então:
E derivando em relação ao tempo:
E então:
Já que a derivada também é a própria velocidade da corrente:
Agora é só substituir:
Passo 3
(b) Agora estamos procurando o valor da aceleração no caso em que , e em que no instante em que .
Dessa vez a aceleração não é constante, então temos que voltar para a nossa equação original:
Quando , a massa do trecho que nos interessa é:
E a taxa de variação da massa é:
E a velocidade é:
Agora é só substituir:
Resolvido!
Resposta
(a) .
(b) .