Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 160
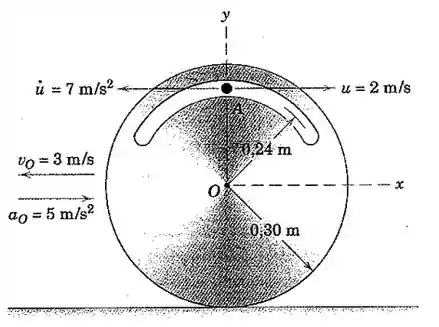
O disco rola sem deslizar sobre a superfície horizontal, e no instante representado, o centro O possui a velocidade e a aceleração mostradas na figura. Para esse instante, a partícula A possui a velocidade indicada u e a taxa de variação no tempo da velocidade , ambos em relação ao disco. Determine a velocidade e a aceleração absolutas da partícula A.
Passo 1
Bom galera, vamos usar o centro O como referencial para os cálculos da velocidade e aceleração de A. Para isso, falta calcularmos a velocidade angular e a aceleração angular do disco:
Beleza! Agora, vamos apresentar os dados da questão em notação vetorial.
Passo 2
Nesta etapa vamos calcular a velocidade e aceleração de A. Primeiro a velocidade:
Agora, vamos para a aceleração:
Resposta
Exercícios de Livros Relacionados
No instante θ = 30 ° , a estrutura do guindaste e a lança A B giram com uma velocidade angular constante ω 1 = 1,5r a d / s e ω 2 = 0,5r a d / s , respectivamente. Determine a velocidade e a aceleraçã
No instante mostrado, a base do braço robótico gira em torno do eixo z com uma velocidade angular ω 1 = 4 r a d / s , a qual está aumentando a ω ˙ 1 = 3r a d / s 2 . Além disso, a lança B C gira com u
Se a manivela B C gira com uma velocidade angular ω B C = 6r a d / s , determine a velocidade do anel em A . Suponha que a velocidade angular de A B é perpendicular à barra.
A barra A B está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A se desloca para cima com uma aceleração a A = 2 km / s 2 , determine a aceleração angular da barra A B e a int
Para o cursor e a manivela do Prob. 5/209 desenvolva a expressão para a aceleração a A do pistão (admitida positiva para a direita) como uma função de θ para ω = θ ˙ = c o n s t a n t e . Substitua os