Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 87
Cada uma das duas hastes da estrutura soldada tem massa de . Um arame desde até impede que a estrutura gire para fora do plano horizontal, em torno de um eixo que passa pelo mancal em e pela rótula em . Calcule a força trativa no arame e o módulo da força total suportada pela rótula em .
Passo 1
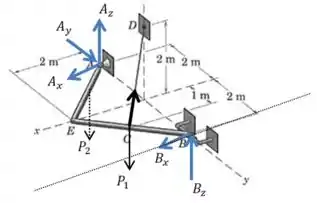
Vamos começar desenhando as forças que atuam no sistema:
Perceba que o suporte em tem uma pequena liberdade para se deslocar ao longo do eixo . Como o sistema está em equilíbrio nessa posição, isso permite concluir que .
Passo 2
Beleza, agora vamos escrever a força em forma vetorial. Precisaremos do vetor unitário na direção (veja o desenho):
E então a força é simplesmente o vetor . Vamos usar alguma equação de equilíbrio que permita calcular .
Se calcularmos o momento em relação ao eixo , todas as forças em e em terão momento nulo, e ficaremos apenas com a componente da força , e :
E todas as forças estão a metro do eixo
:
Mas essa é apenas a componente , podemos usá-la para calcular o valor de :
E isso já resolve o primeiro problema.
Passo 3
Agora queremos calcular o módulo da força suportada em . Mais uma vez vamos ter que montar uma equação de equilíbrio bem pensada para poder resolver a questão.
Vamos escrever uma expressão para o momento em relação à linha que passa pela força :
Nesse casso, as forças , , e , e têm momento nulo, e então a expressão fica da seguinte forma:
E agora vamos fazer a mesma coisa para o momento na direção da força . Nesse caso sobram apenas as forças , e :
Passo 4
E por último podemos usar a condição de equilíbrio das forças na direção do eixo para encontrar :
E então já podemos calcular o módulo da força em :
Resposta
A força trativa no arame é e a suportada pela rótula é .