Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 74
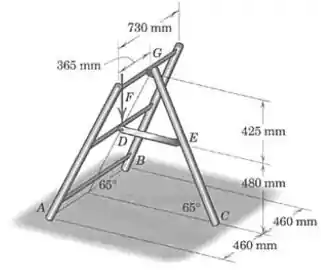
A pequena escada em tripé é útil para apoiar uma extremidade de uma passarela. Se representa o módulo da carga direcionada para baixo causada pela passarela (não mostrada), determine a reação em cada um dos três pés , e . Despreze o atrito.
Passo 1
Temos um total de quatro forças atuando aqui: três reações normais , e , e a força da carga. O que sabemos sobre elas por enquanto?
Bom, as forças e são perfeitamente simétricas (inclusive em relação à força ), então podemos garantir que são iguais:
Ok, como podemos deixar a resposta em função de , isso nos deixa com duas variáveis deconhecidas: e , então vamos precisar montar duas equações.
Passo 2
Vamos começar com o equilíbrio dos momentos. Como escolher o ponto de referência? É uma boa tomar um ponto que anule o momento de uma das forças desconhecidas. Se escolhermos o ponto , por exemplo, a força terá momento nulo:
E temos que considerar os momentos das forças e (em e ). Vamos desenhar uma visão “de lado” da escada:
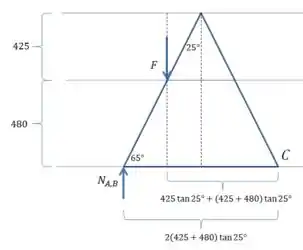
E então o momento em relação ao ponto é:
Passo 3
Agora precisamos de uma segunda equação de equilíbrio. Vamos analisar as forças na direção vertical:
E não esqueça que agora temos que incluir a força :
Pronto.
Resposta
As forças são e .