Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas de Revisão - Ex. 02
Os elementos uniformes e possuem massa de cada e o cilindro possui . Determine a força horizontal necessária para manter o mecanismo em posição quando . A mola tem comprimento não deformado de .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força horizontal necessária para que o corpo fique em equilíbrio com . Sabendo que as hastes e pesam cada e o peso em pesa . Além disso, o comprimento da mola não deformada é de .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
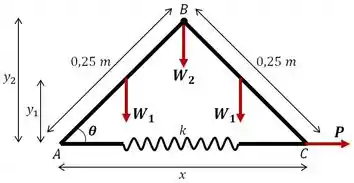
Onde as distâncias , e são:
Passo 2
Show de bola! Para obtermos o deslocamento virtual, precisamos diferenciar , e em relação a :
Para a condição de equilíbrio:
Onde é a força exercida pela mola, que está atuando em no sentido contrário de . Substituindo os valores de e nessa equação:
Passo 3
Para determinar a força exercida pela mola, temos:
Onde a deformação é dada por:
Substituindo na equação do Passo 2:
Como :
Passo 4
Até aqui de boa né? Continuando, como foi dito no enunciado que o corpo está em equilíbrio quando :
É isso, galera. Acabamos mais uma!
Partiu pra próxima!
