Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 59

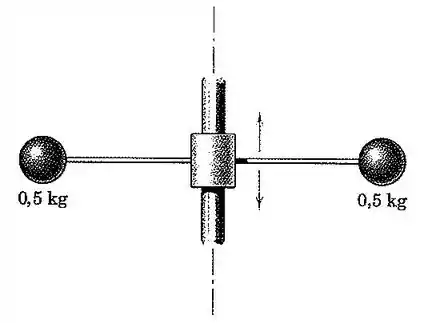
59. Cada uma das esferas de 0,5   k g está presa à extremidade da haste elástica leve e se desloca de 4   m m quando uma força de 2   N é aplicada estaticamente à esfera. Se o cursor central recebe um movimento harmônico vertical com uma frequência de 4   H z e uma amplitude de 3   m m , determine a amplitude y 0 da vibração vertical de cada esfera.

Passo 1

Bom, primeiro a gente vai calcular o equivalente da constante de mola pela relação:

k = P δ

Onde P é a força aplicada e δ é o deslocamento de cada esfera quando a força está aplicada

k = 2 4 × 10 3 m

k = 500   N / m

Passo 2

Agora, vamos calcular a amplitude da vibração vertical y 0 . Como não há nenhum amortecimento no sistema, usaremos a fórmula:

y 0 = b 1 - ω / ω n 2

Aqui, a gente só conhece o valor da amplitude b , que é de 3   m m . Então como acharemos as outras variáveis?

Bom, para achar ω 2 , vamos usar:

ω 2 = ( 4 × 2 π ) 2   ( r a d / s ) 2

Nós tivemos que multiplicar por 2 π porque a frequência estava em H z e a queríamos em r a d / s .

Agora, para achar ω n 2 , usaremos a relação:

ω n 2 = k m

Onde k é o equivalente da constante elástica da mola e m a massa de cada esfera

ω n 2 = 500   N \ m 0,5   k g

ω n 2 = 1000   ( r a d / s ) 2

y 0 = 3   m m 1 - 632   ( r a d / s ) 2 1000   ( r a d / s ) 2

y 0 = 3   m m 1 - 0,632 = 3   m m 0,368

y 0 = 8,15   m m

Resposta

A amplitude y 0 vertical de cada esfera é y 0 = 8,15   m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto executa um MHS com período de 1.200 s e amplitude igual a 0,600 m. Em t = 0, o objeto está em x = O e move-se na direção negativa de x. Qual é a distância entre o objeto e a posição de equil
Um prato uniforme, horizontal, de 1,50 kg, é preso a uma mola vertical ideal de constante igual a 185 N/m, e uma esfera de metal de 275 g está sobre o prato. A mola está sob o prato, podendo oscilar p
Um corpo com massa de 10,0 kg está se deslocando para a direita com uma velocidade igual a 2,00 m/s sobre uma superfície horizontal quando colide com outro corpo que possui massa de 10,0 kg, inicialme
Um objeto com altura h, massa M e seção reta uniforme A flutua diretamente para cima em um líquido com densidade p. (a) Calcule a distância vertical a partir da superfície do líquido até o fundo do ob
Um objeto executa um movimento harmônico simples com período de 0,300 s e amplitude igual a 6,00 cm. Em t = O, o objeto está instantaneamente em repouso em x = 6,00 cm. Calcule o tempo que o objeto le