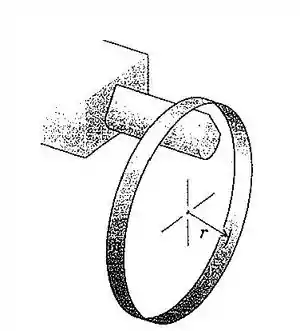
103. Determine o período para o aro circular uniforme de raio , enquanto oscila com pequena amplitude em torno da aresta da cunha horizontal.
Passo 1
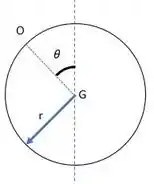
Bom, primeiro vamos montar o diagrama do aro:
Passo 2
E depois bora calcular o momento de inércia do ponto , lembrando que a gente vai ter que usar o teorema dos eixos paralelos:
Como o momento de inércia do aro é e a distância do ponto até o ponto é , temos que:
Passo 3
Agora, vamos relacionar as energias:
Onde é a energia potencial e é a energia cinética
Para a energia cinética, temos:
Mas como
Já para a energia potencial, temos que:
Agora, é só juntar tudo:
Passo 4
Já temos a equação de energia do sistema, agora vamos derivá-la em relação ao tempo para encontrar a equação de posição do aro:
Juntando todas as equações:
Simplificando a expressão e considerando pequeno ():
Passo 5
Como sabemos que a fórmula genérica para a equação de um oscilador harmônico é:
Só que do oscilador harmônico podemos tirar a seguinte relação:
E para calcular a frequência de ressonância precisamos da fórmula:
Passo 6
Agora, para achar o período , vamos usar a fórmula:
Resposta
O período para o aro circular uniforme é: