Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 32

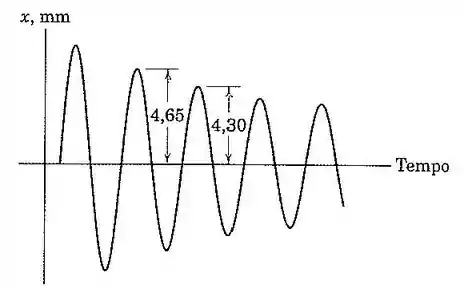
32. Um oscilador harmônico linear que possui uma massa de 1,10   k g é colocado em movimento com um amortecimento viscoso. Se a frequência é de 10   H z e se duas amplitudes sucessivas separadas de um ciclo completo são medidas como 4,65   m m e 4,30   m m , conforme mostrado, calcule o coeficiente de amortecimento viscoso c .

Passo 1

Ora bolas! Se temos duas amplitudes sucessivas separadas por um ciclo completo, o que estamos esperando? Vamos usar a fórmula do decremento logarítmico δ :

δ = ln ⁡ x 1 x 2

Onde x 1 = 4,65   m m e x 2 = 4,30   m m :

δ = ln ⁡ 4,65   m m 4,30   m m

δ ≅ 0,0783

Passo 2

Agora vamos usar a seguinte fórmula abaixo, que relaciona o decremento logarítmico δ com o fator de amortecimento 𝜉.

ξ = δ ( 2 π ) 2 + δ 2

E substituimos o valor numérico de δ :

ξ ≅ 0,0783 ( 2 π ) 2 + ( 0,0783 ) 2

ξ ≅ 0,01245

Passo 3

Uma vez obtido o fator de amortecimento, sabemos que ele está relacionado com o coeficiente c de amortecimento, pela fórmula abaixo:

ξ = c 2 m ω n

c = 2 m ξ ω n

Trocando os valores pertinentes a cada variável, alcançamos nosso resultado.

c ≅ 2 ( 1,10   k g ) ( 0,01245 ) ( 2 π ⋅ 10   H z )

c ≅ 1721   N ⋅ s m

Resposta

c ≅ 1721   N ⋅ s m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?
O sistema de suspensão de um automóvel de 2000 k g “cede” 10 c m quando o chassis é colocado no lugar. Além disso, a amplitude das oscilações diminui de 50 % a cada ciclo. Estime o valor (a) da consta
Na Fig 15-14 o bloco possui uma massa de 1,50 k g e a constante elástica é 8,00 N / m . A força de amortecimento é dada por - b d x / d t , onde b = 230 g / s . O bloco é puxado 12,0 c m para baixo e
Verdadeiro ou falso:A energia mecânica de um oscilador amortecido, decresce exponencialmente com o tempo.A ressonância para um oscilador amortecido forçado ocorre quando a frequência da força externa
Dois sistemas massa-mola amortecidos forçados oscilando possuem massas, forças externas e constantes de amortecimento idênticas. Porém, a constante de força k A do sistema A é quatro vezes a constante