Um cabo homogêneo de comprimento e seção transversal uniforme é preso por uma de suas extremidades. (a) Expressando por a densidade (massa por volume) do cabo e por o módulo de elasticidade, determinar o alongamento do cabo, devido ao seu próprio peso; (b) Mostre que o mesmo alongamento poderá ser obtido se o cabo fosse horizontal e se uma força igual à metade do seu peso fosse aplicada na extremidade do cabo.
Passo 1
Existem duas formas de resolver essa questão. Uma delas consiste em considerar um elemento de comprimento infinitesimal na barra, aplicar a equação 2.7 neste elemento e depois integrar ao longo da barra.
Porém a densidade da barra é constante, e por isso não vamos precisar utilizar integrais! Podemos resolver essa questão apenas utilizando nossos conhecimentos sobre o comportamento da força peso.
Abaixo a gente tem o desenho do cabo. Vamos dizer que esse cabo tem uma seção transversal de área .

A única força que atua sobre o cabo é o peso do cabo. A força peso é:
E como sabemos, a força peso de um objeto sempre atua no meio do objeto:
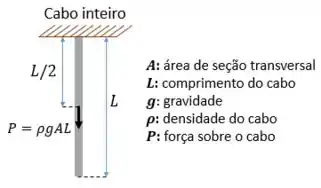
Passo 2
Como a força atua na metade do cabo, então podemos considerar que apenas metade do cabo está sendo esticado. Vamos calcular a deformação: