Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 122

Cada um dos membros da treliça mostrada é feita de aço e tem a área da seção transversal indicada. Usando-se E = 200 G P a ,   determinar a deflexão vertical do nó C.

Passo 1

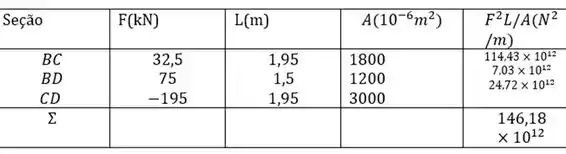
E ai galera vamos começar determinando o comprimento e em seguida os somatórios das forças, vem comigo :D

l B C = l C D = 1,8 2 + 0,75 2 = 1,95 m

J u n t a   C

+ → Σ F x = 0 :   - 1,8 1,95 F B C - 1,8 1,95 F C D + 120 = 0       1

+ ↑ Σ F y = 0 : 0,75 1,95 F B C - 0,75 1,95 F C D - 200 = 0       2

Passo 2

R e s o l v e n d o   1   e   2 s i m u l t a n e a m e n t e  

F B C = 325   k N         F C D = - 195 k N

+ ↑ Σ F y = 0 : F B D + 0,75 1,95 F C D = 0       F C D = 75 k N

U = Σ F 2 L 2 E A = 1 2 E Σ F 2 L A

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Considerando que a viga prismática AB tem uma seção transversal retangular, mostre que para a carregamento indicado o valor máximo da densidade de energia de deformação na viga é M m a z = 45 8 U V Em
Na montagem mostrada, os torques T AeT B são aplicados nos discos A e B, respectivamente. Sabendo que ambos os eixos são maciços e feitos de alumínio ( G = 73G P a ) , determine a energia de deformaçã