Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 125

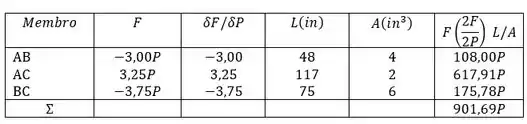
Cada um dos membros da treliça mostrada é feita de alumínio e tem a área da seção transversal indicada. Usando E = 70 G P a ,   determinar a deflexão vertical do nó C.

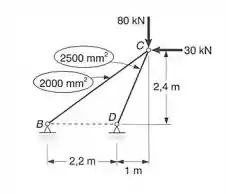
Passo 1

Chame a carga vertical de P. A deflexão vertical da junto C é δ P

δ P = 2 U 2 P = 2 2 P Σ F 2 L 2 E A = 1 E Σ F L A 2 F 2 P

Geometria A C - = 9 2 + 3,75 2 = 9,75 f t = 117 i n

B C - = 5 2 + 3,75 2 = 6,25 f t = 75 i n

4 f t = 48 i n .   ,   5 f t = 60 i n ,   3,75 f t = 45 i n

Passo 2

Junta C

+ → Σ F x = 0         - 108 117   F A C - 60 75   F B C = 0

+ ↑ Σ F y = 0     - 45 117   F A C - 45 75 F B C - P = 0

Resolvendo simultaneamente F A C = 3,25 P ,   F B C = - 3,75 P

Junta B + → Σ F A B = 0         - F A B - 6 P 75 F A C = 0

F A B = - 3,00 P .

Passo 3

δ P = 901,69 P E = 901,69 7,5 × 10 3 29 × 10 6 = 0,233 i n ↓

Resposta

0,233

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre por integração que a energia de deformação na barra cônica AB é U = 7 48 T 2 L G J m i n em que J m i n é o momento polar de inércia na barra na extremidade B.
A s especificações de projeto para o eixo de aço AB exigem que o eixo absorva uma energia de deformação de 400i n ∙ l b enquanto se aplica um torque de 25 k i p ∙ i n . Utilizando G = 11,2 × 10 6 p s
σ E = 160 M P a . Usando o critério da máxima energia de distorção , determine o intervalo de valores de σ z para o qual não ocorre o escoamento.
σ E = 448 M P a . Usando o critério da máxima energia de distorção, determine o intervalo de valores de σ y para o qual o coeficiente de segurança associado à tensão de escoamento é igual ou maior do
O estado de tensão mostrado na figura ocorre em um componente de máquina feito de um tipo de aço para o qual σ E = 448M P a . Usando o critério da máxima energia de distorção, determine o coeficiente