Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 7

Cada uma das quatro barras verticais tem uma seção transversal retangular uniforme de 8 x 36 mm e cada um dos quatro pinos tem um diâmetro de 16 mm. Determine o valor máximo da tensão normal média dos vínculos que conectam (a) pontos B e D, (b) pontos C e E

Passo 1

E ai gurizada tudo belezinha??? Antes de qualquer coisa vamos desenhar o diagrama de corpo livre para visualizarmos melhor o exercício.

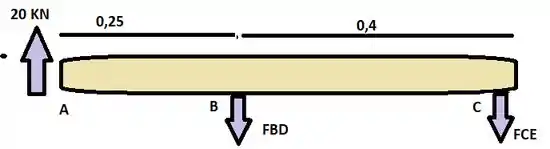
Agora vamos calcular primeiramente o somatório do momento em c :D

+ ↺ ∑ M c = F × d = 0

0,4 F B D - 0,25 + 0,4 × 20 × 10 3 = 0

F B D = 32500   N

O mesmo faremos para o momento em B

+ ↺ ∑ M B = F × d = 0

- 0,4 F C E - 0,25 × 20 × 10 3 = 0

F C E = - 12500   N

Passo 2

Gurizada agora para encontrarmos as tensões nas diferentes regiões vamos relembrar a equação:

σ B D = F A

Mas notem que ainda não calculamos a área então antes de determinar a tensão partiu calcular a área...

A = 0,008 × 0,036 - 0,016 = 160 × 10 - 6 m 2

como são duas partes paralelas multiplicaremos por 2 e teremos = 320 × 10 - 6 m 2

Agora sim podemos calcular:

σ B D = 32500 320 × 10 - 6 = 101,56   M P a

Passo 3

σ C E = F A

Mas notem que ainda não calculamos a área então antes de determinar a tensão partiu calcular a área...

A = 0,008 × 0,036 = 288 × 10 - 6 m 2

como são duas partes paralelas multiplicaremos por 2 e teremos = 576 × 10 - 6 m 2

Agora sim podemos calcular:

σ C E = - 12500 576 × 10 - 6 = - 21,7   M P a

Resposta

  1. 101,56   M P a
  2. - 21,7   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força axial centrada e aplicada à barra de aço mostrada. Sabendo que σ m i n = 20k s i , determine a máxima carga P admissível.
A barra retangular AB, com lado de 30 mm, tem comprimento L = 2,5m e é feita de um aço doce considerado elastoplástico com E = 200G P aeσ E = 345M P a . Uma força P é aplicada à barra e em seguida rem
A barra ABC consiste em duas parte cilíndricas AB e BC: ela é feita de um aço doce considerado elastoplástico com E = 200G P aeσ E = 250M P a . Uma força P é aplicada à barra até que sua extremidade A
Resolva o Problema 2.103 supondo que a tensão de escoamento do aço doce seja de 250 MPa.
A barra AB é feita de um aço doce considerado elastoplástico com E = 200G P ae σ E = 248M P a . Depois de a barra ter sido lixada a uma alavanca rígida CD, descobriu-se que a extremidade C está 9,53 m