Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 87
Cada uma das quatro rodas do veículo tem uma massa de 20 kg e está montada em um eixo de 80 mm de diâmetro. A massa total do veículo é 480 kg, incluindo as rodas, e está distribuída igualmente pelas quatro rodas. Se uma força N é necessária para manter o veículo rodando sob uma velocidade constante baixa sobre uma superfície horizontal, calcule o coeficiente de atrito que existe nos mancais das rodas. (Sugestão: Desenhe um diagrama de corpo livre completo para uma roda.)
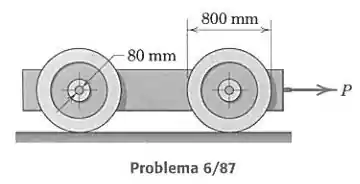
Passo 1
Primeiro, vamos desenhar o diagrama de corpo livre para uma roda. Primeiro temos o peso da roda, aplicado em seu centro, igual a . Temos uma força normal aplicada pelo solo que equilibra um quarto do peso total do veículo, igual a e uma força de atrito para trás, que faz a roda girar. Como o carro anda a velocidade constante, a resultante das forças horizontais deve ser zero, então cada força de atrito nas rodas deve ser igual a 20 N para compensar a força de 80 N aplicada para puxar o veículo. Além disso, temos a força aplicada pelo eixo nos mancais. Essa força deve fazer um ângulo de atrito com a normal à superfície de contato, tal que:
Sendo o coeficiente de atrito entre o eixo e o mancal.
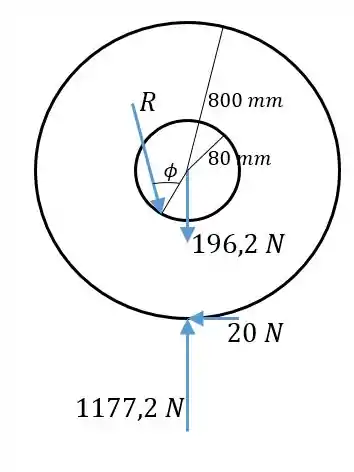
Passo 2
Um jeito fácil de resolver esse diagrama de corpo livre é ignorar a força peso da roda e a parte da normal feita pelo solo que equilibra esse peso. A força normal do solo fica então
E temos o nosso diagrama de corpo livre modificado:
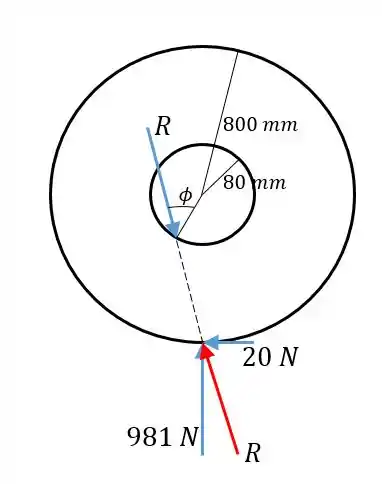
Agora, pelo equilíbrio de forças horizontal e vertical e pelo momento em torno do ponto de contato com o chão igual a zero, sabemos que as duas resultantes são colineares e iguais. Então:
Então fazemos o momento em torno do centro ser zero. A força de 20 N causa momento horário e a componente da força entre o eixo e o mancal que causa o momento é tangente ao círculo de raio 80 mm e possui nessa direção componente . Então:
Pela relação fundamental trigonométrica, encontramos o cosseno de :
Então encontramos :