Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 34
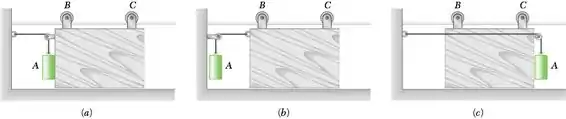
Um painel deslizante de 40 kg é suportado pelos roletes em B e C. Um contrapeso A de 25 kg é fixado por cabo como mostrado na figura e, nos casos a e c, estão em contato com a borda vertical do painel. Desprezando o atrito, determine em cada caso mostrado a aceleração do painel e a tração na corda imediatamente depois do sistema sair do repouso.
Passo 1
E ai tudo certinho? O enunciado pede que a gente determine em cada caso mostrado a aceleração do painel e a tração na corda imediatamente depois do sistema sair do repouso. Começaremos pelo painel A
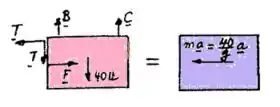
- Painel:
- Painel:
F = Força exercida pelo contrapeso
Contrapeso A: sua aceleração tem dois componentes
Adicionando (1), (2) e (3)
Substituindo a em (3):
Passo 2
Contrapeso A:
Adicionando (1) e (2):
Substituindo a em (1)
Passo 2
Como o painel é acelerado para a esquerda, não há força exercida pelo painel no contrapeso e vice-versa.
Painel:
Contrapeso A: Mesmo corpo livre como na Parte (b):
Como as Eqs. (1) e (2) são os mesmos que em (b), obtemos as mesmas respostas: