Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 66
Durante um teste de impacto, o peso de é liberado do repouso quando . Ele oscila para baixo e atinge os blocos de concreto, ricocheteia e oscila de volta com antes de parar momentaneamente. Dtermine o coeficiente de restituição entre o peso e os blocos. Além disso, determine o impulso transferido entre o peso e os blocos durante o impacto. Suponha que os blocos não se movem após o impacto.
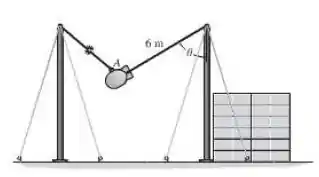
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de energia, temos:
O coeficiente de restituição é dado por:
Aplicando o principio do impulso e quantidade de movimento para o bloco :
Resposta
Exercícios de Livros Relacionados
Uma espaçonave de 600 kg é colocada primeiramente em uma órbita circular em torno da Terra a uma altitude de 4.500 km e, então, transferida para uma órbita circular em torno da Lua. Sabendo que a mass
A haste 0A oscila cerca de 0 em um plano horizontal. O movimento do colar B de 5 lb é definido pelas relaçõesr = 10 / ( t + 4 ) and θ = ( 2 / π ) s i n π t , onde r é expresso em pés, t em segundos
Um colar de 1,5 kg pode deslizar em uma haste horizontal que é livre para girar sobre um eixo vertical. O colar é inicialmente mantido preso ao eixo em A por uma corda. A mola de constante 35 N/m é fi
Para colocar um satélite de comunicações em uma órbita geossíncrona (ver Problema 12.80) a uma altitude de 35.580 km acima da superfície da Terra, o satélite primeiro é liberado do ônibus espacial, cu
Planos para a missão de um pouso não tripulado ao planeta Marte indica que o veículo de retorno à Terra primeiro descreve uma órbita circular a uma altitude dA × 2.200 km acima da superfície do planet