Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 69

Determine os momentos de inércia I U , I v e o produto de inércia I U V da área retangular.

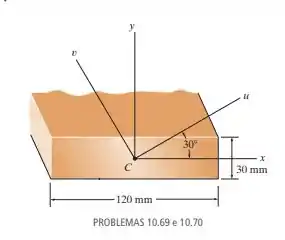
Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, vamos determinar os momentos de inércia em cada eixo:

I y = 30 × 120 3 12 = 4320000   m m 4

I x = 120 × 30 3 12 = 270000   m m 4

Sabemos que:

I u = I x + I y 2 + I x - I y 2 cos ⁡ 2 θ

I v = I x + I y 2 + I x - I y 2 sen ⁡ 2 θ

I u v = I x - I y 2 cos ⁡ 2 θ

Portanto, substituindo:

I u = 1282500

I v = 541298,55

I u v = - 1012500

Resposta

I u = 1282500

I v = 541298,55

I u v = - 1012500

I y = 378333,33   m m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine y - , que localiza o eixo centroidal x ' da área da seção transversal da viga “ T ” , e depois calcule o momento de inércia em relação ao eixo x ' .
67. Determine os momentos de inércia I u e I v da área sombreada.
Determine o momento de inércia do anel fino em relação ao eixo z . O anel tem massa m .
Determine a orientação dos eixos principais, que têm sua origem no ponto C , e os momentos de inércia principais da seção transversal em relação a esses eixos.
Resolva o Problema 10.69 usando o círculo de Mohr.