Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 16

A caixa de 100 kg é içada pelo motor M . O motor excerce no cabo uma força

T = 200 t 1 / 2 + 150   N

onde t está em segundos. Se a caixa parte do repouso no solo, determine a velocidade da caixa quando t = 5 s.

Passo 1

O enunciado nos dá as seguintes informações:

Massa da caixa: m = 100   k g ;

Velocidade inicial: v 0 = 0 m/s;

Tempo de aceleração: t = 5 s;

Tração no cabo: T = 200 t 1 / 2 + 150   N .

Devemos determinar a velocidade v   da caixa no instante t = 5 s.

Para facilitar nossa resolução, vamos desenhar o diagrama de corpo livre da caixa:

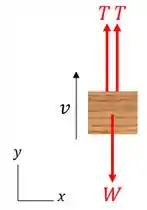
Onde T é a força de tração exercida pelo cabo e W = m g é a força peso.

Passo 2

Como a caixa parte do repouso, o cabo deve fazer força suficiente para tirá-la da inércia, ou seja, deve vencer o peso incial da caixa. Isso demandará alguns segundos. Vamos aplicar a Equação do Movimento no eixo y para descobrir o tempo necessário para fazer com que a caixa comece a se mover. Neste momento a aceleração tenderá a zero, pois a caixa estará na iminência de iniciar o movimento., logo a = 0 .

∑ F y = m a y

T + T - m g = m 0

2 T = 100 9,81

T = 490,5

200 t 1 2 + 150 = 490,5

t 1 / 2 = 1,7025

t = 2,89 85   s

Neste instante, a caixa passa a ter uma velocidade maior que zero.

Passo 3

Para encontrar a velocidade v , vamos aplicar o Princípio do Impulso e Quantidade de Movimento Linear:

∑ m i v i 1 + ∑ ∫ t 1 t 2 F i d t = ∑ m i v i 2

No eixo y   entre os instantes   t = 2,8985   e   t = 5   s , pois é nesse momento que a caixa tem velocidade não nula:

m v 0 + ∑ ∫ 2.8985 5 F y d t = m v

100 0 + ∫ 2.8985 5 2 T - W d t = 100 v

0 + ∫ 2.8985 5 2 200 t 1 / 2 + 150   - W d t = 100 v

400 2 3 [ 5 3 / 2 - 2.8985 3 / 2 ] + 300 [ 5 - 2.8985 ] - 100 9,81 [ 5 - 2.8985 ] = 100 v

v = 2,34   s

Resposta

v = 2,34   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O piloto de um avião de 40t que está originalmente voando horizontalmente a uma velocidade de 650k m / h corta toda a potência do motor e entra em uma trajetória de 5 ° de vôo planado como mostrado. A
O martelo com 450k g de um bate-estaca cai 1,4m a partir do repouso e atinge o topo de uma estaca de 240k g enterrada 0,9m no solo. Após o impacto observa-se o martelo se deslocar com a estaca sem ric
A partícula de 2,4k g se desloca no plano horizontal x y e tem a velocidade mostrada no instante de tempo t = 0 . Se a força F = 2 + 3 t 2 / 4 newtons, onde t é o tempo em segundos, é aplicada à partí
O superpetroleiro tem um deslocamento (massa) total de 150 ( 10 3 ) toneladas métricas (uma tonelada métrica é igual a 1000k g ) e está parado na água quando o rebocador começa a puxar. Se uma tração
O bloco de 10k g está se deslocando para a esquerda com uma velocidade de 1,2m / s no instante de tempo t = 0 , quando a força P é aplicada como mostrado no gráfico. A força continua no nível de 10N .