Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 48
Um automóvel tendo massa de 1750 kg sobe um aclive de a uma velocidade constante de m/s. Se o atrito e a resistência do vento são desprezados, determine a potência desenvolvida pelo motor se o automóvels tem uma eficiência mecânica de
Passo 1
O enunciado nos dá as seguintes informações:
Massa do automóvel: ;
Velocidade constante: m/s;
Eficiência: .
Devemos determinar a potência máxima desenvolvida pelo motor deste automóvel sabendo que ele possui eficiência .
Vamos desenhar o diagrama de corpo livre do automóvel para visualiza melhor seu movimento:
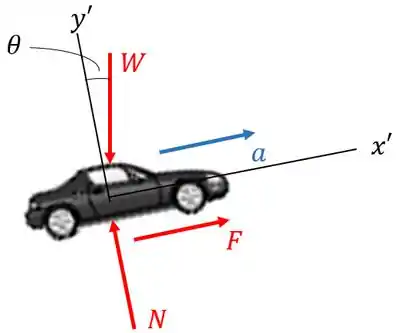
Onde é a força peso, é a força exercida pelo motor do carro e é a força normal.
Sabemos que e que , pois a velocidade é constante.
Passo 2
Por definição, sabemos que a velocidade é igual a variação do espaço sobre a variação de tempo, logo
Vamos assumir que a posição inicial do carro seja e que, para uma variação de segundo, o automóvel percorra uma distância igual a . Logo, temos que
Passo 3
Em seguida, vamos determinar o trabalho realizado pelo motor.
Sabemos que o trabalho é igual a força vezes o deslocamento. Na direção do deslocamento, temos apenas a ação da componente em da força peso.
Logo, do instante para o instante , temos que
Portanto, temos que a potência para o instante s é de
Esta é a potência necessária para fazer com que o carro consiga manter sua velocidade nesse deslocamento. Podemos chamá-la de Potência de Saída, uma vez que é a potência mínima que o motor precisará fornecer.
Para encontrar a potência de entrada, devemos utilizar a informação sobre a eficiência do motor.
Passo 4
Sabemos que a eficiência é definida por
Portanto, a potência de entrada é dada por
Logo, temos que