Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 202
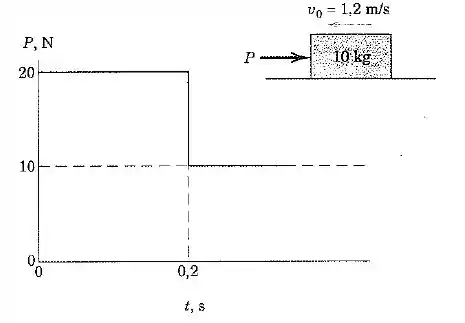
O bloco de está se deslocando para a esquerda com uma velocidade de no instante de tempo , quando a força é aplicada como mostrado no gráfico. A força continua no nível de . Se o coeficiente de atrito dinâmico é , determine o tempo no qual o bloco para.
Passo 1
Vamos começar analisando o movimento naqueles primeiros . Como o bloco está se movendo para a esquerda, a força e o atrito apontam no mesmo sentido:
Então essa é a força resultante que age sobre o bloco nos primeiros , vamos ver qual é a variação de velocidade gerada:
E como a velocidade inicial do bloco era (atenção para o sinal!), a nova velocidade é:
Passo 2
A partir do teremos apenas o atrito e uma força tentando parar o bloco, de forma que a força resultante é:
Lembrando que ele tinha velocidade , vamos ver quanto tempo ele demora para parar. A variação de momento tem que ser a seguinte:
E agora vamos usar o teorema do impulso:
E quando também consideramos aqueles primeiros de movimento, concluímos que o instante em que o bloco para é:
Resposta
O bloco leva para parar.