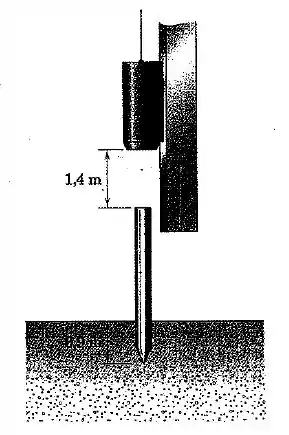
O martelo com de um bate-estaca cai a partir do repouso e atinge o topo de uma estaca de enterrada no solo. Após o impacto observa-se o martelo se deslocar com a estaca sem ricochetear visivelmente. Determine a velocidade da estaca e do martelo imediatamente após o impacto. Você pode justificar o uso do princípio da conservação da quantidade de movimento embora os pesos atuem durante o impacto?

Ok, agora precisamos considerar que esse martelo se “junta” à estaca, e queremos saber qual é a velocidade com que os dois se movem. Pela conservação de momento linear, temos:

E agora falta responder a última pergunta: o que nos deu o direito de usar a conservação de momento linear?

Afinal de contas, o sistema não é isolado! Temos a força peso agindo, o que deveria mudar a quantidade total de movimento do sistema, afinal de contas:

Bom, lembre-se de que só usamos a conservação para o pequeno intervalo da colisão entre o martelo e a estaca, e não para a queda do martelo.

Nesse caso, as forças de impacto entre a estaca e o martelo são muito superiores ao efeito da força peso, especialmente em um intervalo de tempo tão curto.