Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 182
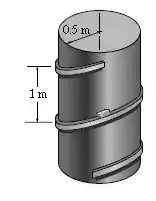
A caixa desce deslizando pela rampa helicoidal com uma velocidade escalar constante de . Determine a intensidade da sua aceleração. A rampa desce uma distância vertical de para cada volta completa. O raio médio da rampa é
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado nos pede a intensidade da sua aceleração.
Podemos definir o ângulo de inclinação da rampa como:
Analisando o diagrama abaixo, temos:
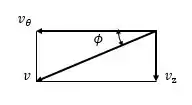
Como é constante, .
Passo 2
Sabemos que:
Logo:
Como dito anteriormente, é constante, logo e valem zero. Temos também que é constante, portanto . Temos o mesmo caso para que é uma constante, então .
Como:
Temos que:
Resposta
Exercícios de Livros Relacionados
Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se a sua posição é θ ˙ = 3 t 2 rad/s, onde t é dado em segundos, determine as instensidades da velocidade e aceleração da part
2/112 ) Um carro faz uma curva de curvatura constante entre A e B com uma velocidade também constante de 45 quilômetros por hora . Se um acelerômetro foi montado no carro , qual módulo da aceleração e
2/110) Considere o eixo polar da terra como fixo no espaço e calcule o módulo da aceleração a de um ponto P sobre a superfície da terra a uma latitude de 40 ° norte . O diâmetro médio da terra é 12742
2/109 ) A figura mostra duas trajetórias possíveis para passar por uma curva sem inclinação lateral em uma parte horizontal de uma pista de corrida . A trajetória A-Asegue a linha central da estrada e
2/114) Uma nave espacial S está em órbita de júpiter em uma trajetória circular de 1000k m acima dasuperfície com umavelocidade constante . Utilizando a lei gravitacional , calcule omódulo v de sua ve