Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 8
Um caixote de está apoiado na porta de da caçamba de uma picape. Calcule a força trativa em cada um dos dois cabos de sustentação, um dos quais é mostrado. Os centros de gravidade estão em . O caixote está localizado a meia distância entre os dois cabos.
Passo 1
Pessoal, podemos tratar o problema como bidimensional, já que o caixote está a meia distância entre os dois cabos. Então, fazendo um ângulo com a horizontal, consideraremos uma força trativa equivalente de , conforme mostra a figura a seguir:
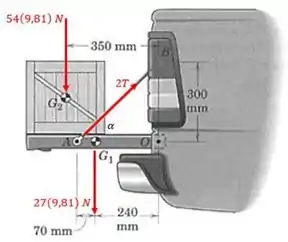
Usando as dimensões da figura, vamos calcular o ângulo
Passo 2
Como o sistema está em equilíbrio, sem girar, podemos dizer que o somatório dos momentos das forças em torno de é nulo:
As forças com momento não nulo em torno de são os pesos do caixote e da porta (sentido anti-horário), além da força trativa (sentido horário):
Pronto, tá finalizado nosso problema.