Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 102
A estrutura é usada para sustentar o cilindro de . Determine a força do pino em sobre o membro e sobre o membro .
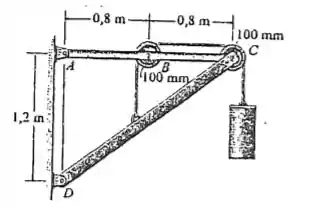
Passo 1
Como o enunciado foi bem direto com relação ao que desejava, vamos esboçar o seguinte diagrama de forças para o nosso problema:
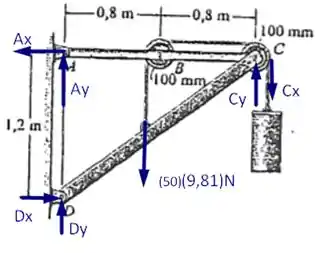
Das equações de equilíbrio e adotando o sentido anti-horário como o positivo vamos ter
Passo 2
Dessa forma, podemos calcular o valor de . Agora, precisamos calcular que vem da polia. Assim, teremos
Sendo assim, da mesma forma como fizemos para poderemos fazer para acharmos , então,
Resposta
Exercícios de Livros Relacionados
O guincho da ponte rolante está projetado para uma capacidade máxima de 10k N e a viga em I uniforme tem uma massa de 200k g . (a) Faça um gráfico do módulo R da força no pino em A em função de x , ao
Dois sinais de trânsito estão presos, em intervalos iguais, ao cabo de sustentação de 10,8m de comprimento, como mostrado. Determine os ângulos α , β e γ da configuração de equilíbrio, bem como a forç
Os dois sinais de trânsito do Prob. 3/118 foram, agora, reposicionados de modo que o segmento B C do cabo de sustentação de 10,8m tem 3m de comprimento e está na horizontal. Especifique os comprimento
Desenhe o diagrama de forças da bobina de papel de 50 kg que possui um centro de massa em G e se apoia sobre uma lamina lisa da empilhadeira. Explique o significado de cada força no Diagrama
Desenhe o diagrama de Corpo Livre da chave, sujeita a uma força de 100N. O apoio em A pode ser considerado um pino e a superfície de contato em B é lisa. Explique o significado de cada força no Diagra