Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 116
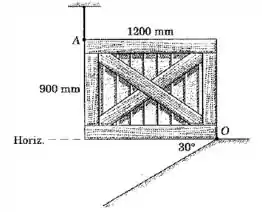
O caixote retangular homogêneo possui uma massa de e está sustentado na posição horizontal pelo cabo em e pela dobradiça no canto . Se o cabo em é liberado repentinamente, calcule a velocidade angular do caixote pouco antes que atinja a inclinação de . O peso do caixote influencia os resultados, com outras grandezas invariáveis?
Passo 1
O que vai acontecer aqui é o seguinte: a energia potencial gravitacional vai se converter em energia cinética de rotação em torno do ponto . Vamos escrever isso matematicamente:
E nosso problema é encontrar expressões para a altura pela qual o centro de massa cai, e para o momento de inércia do caixote.
Vamos começar pelo momento de inércia, que é tabelado para um bloco retangular:
Substituindo isso na equação de cima e isolando , encontramos o seguinte:
Passo 2
Agora só falta encontrar a altura . Vamos precisar de algumas considerações geométricas:
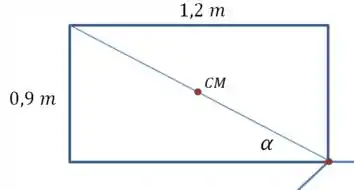
Começamos calculando esse ângulo da diagonl:
E podemos calcular também a distância entre o ponto de apoio e o centro de massa, usando o teorema de pitágoras:
Isso quer dizer que, quando a linha do centro de massa se inclinar por , teremos algo parecido com isso:
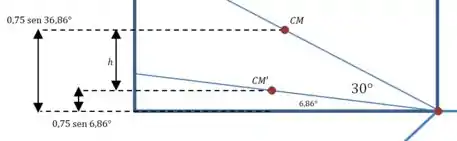
Então:
Agora é só substituir na equação que escrevemos no passo anterior:
Passo 3
O enunciado também perguntou se o peso do caixote influencia nos resultados. Vamos dar mais uma olhada na nossa equação, mas dessa vez sem os valores numéricos:
Mas podemos reescrever sempre será a massa multiplicada por algum comprimento ao quadrado:
Então:
Ou seja, a massa se cancela, e portanto o peso não interfere no resultado.
Resposta
A velocidade angular será , e o peso não interfere no resultado.