Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 122

A estrutura quadrada é composta por quatro hastes esbeltas, cada uma de massa m e comprimento b . A estrutura está girando em seu plano com uma velocidade angular ω . Determine a velocidade linear v do centro C , que fará a energia cinética de translação igual à energia cinética de rotação.

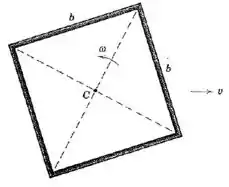
Passo 1

Vamos começar encontrando uma expressão para o momento de inércia em relação a um eixo que passa pelo ponto C .

O sistema é composto por quatro hastes esbeltas iguais, então vamos escrever esse momento de inércia da seguinte forma:

I C = 4 I h a s t e

Onde o momento de inércia de cada haste pode ser escrito com o teorema dos eixos paralelos:

I h a s t e = I c m + m d 2

I h a s t e = 1 12 m b 2 + m b 2 2 = 4 12 m b 2

Então:

I C = 4 4 12 m b 2 = 16 12 m b 2 = 4 3 m b 2

Passo 2

E então a energia cinética de rotação fica da seguinte forma:

T r o t = 1 2 I C ω 2 = 1 2   4 3 m b 2 ω 2

T r o t = 2 3 m b 2 ω 2

E para a energia cinética de translação:

T t r a n s = 1 2 4 m v 2 = 2 m v 2

O que queremos saber é a velocidade v que permite a seguinte igualdade:

T t r a n s = T r o t

2 3 m b 2 ω 2 = 2 m v 2

v = b ω 3

Resposta

Essa igualdade acontece quando v = b ω / 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 18.12, se o coeficiente de atrito cinético entre a bobina e o plano em A for μ k = 0,2 .
Se o sistema é solto do repouso, determine a velocidade dos cilindros de 20 kg, A e B, após A ter se deslocado para baixo uma distância de 2 m. A polia diferencial tem massa de 15 kg e raio de giração
A tampa da caixa de 6 kg é mantida em equilíbrio pela mola torsional em θ = 60 ° . Se a tampa é forçada a fechar-se, θ = 0 ° , e em seguida é liberada, determine sua velocidade angular no instante em
A roda e a bobina a ela fixada têm uma massa combinada de 25 kg e raio de giração em relação a seu centro k A = 150m m . Se a polia B, que está fixada ao motor, for sujeita a um torque M = 75N . m , d
Determine a velocidade angular das duas barras de 10 kg quando θ = 180 ° , se elas são liberadas do repouso na posição θ = 60 ° . Despreze o atrito.