Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 11

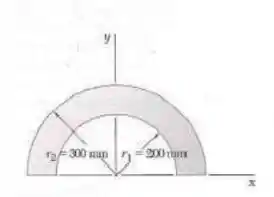
Calcule o centroide da área a seguir:

Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o centroide da área dada. Para isso, vamos dividir a área em figuras conhecidas.

Logo, o centroide será o produto do centroide dosemicirculo maior pela sua área menos o produto do centroide do semicírculo menor pela sua área, dividido pela área do maior menos a área do menor. Como há simetria em x, sabemos que o overset(-)(x) = 0 . Logo:

A xx overset(-)(y)_s e m i c i r c u l o 1 = 4 xx (300)/(3 pi) xx (1)/(2) xx pi xx 300^2 = 18000000

Já o dopequeno será:

A xx overset(-)(y)_s e m i c i r c u l o 2 = 4 xx (200)/(3 pi) xx (1)/(2) xx pi xx 200^2 = 5333333,333

Portanto:

overset(-)(x) = 0

overset(-)(y) = (12666666,67)/(157079,6327) = 80,63 m m

Resposta

overset(-)(x) = 0

overset(-)(y) = 80,63 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

24- Determine as coordenadas do centroide da área sombreada
25- Determine as coordenadas x e y do centroide da área sombreada.
2- Faça com seu lápis um ponto sobre a posição da sua melhor estimativa visual do centroide da área do setor circular. Verifique sua estimativa usando os resultados do Exercício 5/3.
Localize o centroide da área sombreada entre as duas curvas.
Determine a coordenada y do centroide da área sombreada