Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 90
Três barras de controle são fixadas a uma alavanca ABC e exercem forças sobre ela como mostrado na figura. Substitua as três forças por um sistema força-binário em B. Determine uma única força que equivale ao sistema força-binário obtido na parte e especifique seu ponto de aplicação na alavanca.
Passo 1
Vamos começar o exercício desenhando o diagrama de corpo livre para o sistema:
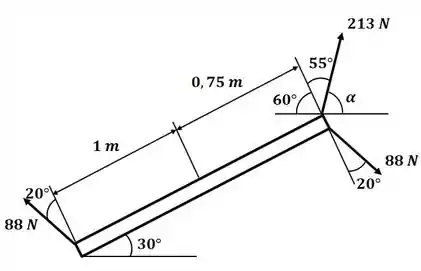
Precisamos substituir as forças no sistema por um momento e uma força resultante, como as forças de 88 N formam um binário, então, calculando o somatório de momento em relação ao ponto B teremos um momento resultante para o sistema equivalente:
Passo 2
Esse será nosso binário resultante. Agora, a força será a força aplicada no ponto C, com o mesmoo módulo de 213 N. Para determinar sua direção, precisamos encontrar o ângulo que ela faz com a horizontal, dessa forma, olhando para o DCL, temos:
Então, a força é:
Passo 3
Agora para a letra queremos uma única força sendo aplicada no sistema, então, conforme vimos na letra , a força deve ter o seguinte módulo e direção:
Agora, para descobrir o ponto de aplicação , devemos igualar o momento binário encontrado na letra com a direção da força , lembrando que como o momento está no sentido horário, devido a direção da força (65° com a horizontal), sabemos que ela deve ser aplicada a esquerda do ponto B, então, dessa forma:
Então o ponto de aplicação fica a a esquerda do ponto B.