Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 36

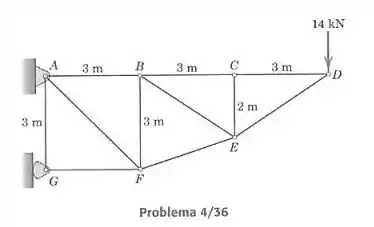
Calcule as forças nos elementos , . Determine cada força a partir de uma equação de equilíbrio que a contenha como a única incógnita.

Passo 1

Vamos calcular as forças pelo método das seções, dividindo a treliça em duas e tratando uma parte dela como se fosse um corpo rígido. Estamos interessados nos elementos , e , então devemos fazer um corte passando por esses três elementos. Para resolver cada força com uma equação tendo apenas ela como incógnita, devemos ter as outras duas forças passando pelo mesmo ponto e fazer a equação da soma dos momentos ao redor desse ponto, porque assim essas duas outras forças não aparecem na equação. Então devemos achar as interseções das linhas de ação das forças.

Passo 2

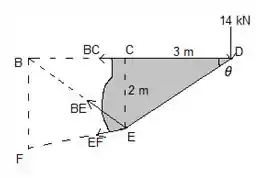
Nosso desenho fica assim:

Passo 3

Para obter , devemos calcular o momento em torno do ponto de interseção da linha de e . Esse é o ponto , então:

Passo 4

Para calcular , percebemos que as linhas de e passam por . Devemos calcular o ângulo que faz com a horizontal:

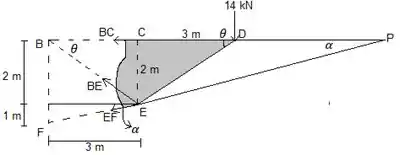
Agora fazemos a a soma dos momentos em torno de ser zero:

Substituindo o seno e o cosseno:

O sinal negativo indica que a força no elemento é de compressão e não de tração como supomos no desenho.

Passo 5

Agora só falta calcularmos . e se cruzam no ponto mostrado na figura. Precisamos da distância de a e do ângulo entre e a horizontal para fazermos a equação do momento em torno de . Fazemos assim: