Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 37

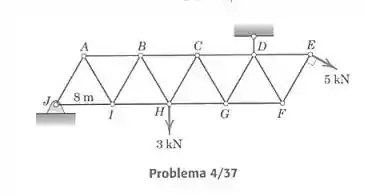
Calcule as forças nos elementos , e da treliça carregada, formada por triângulos equiláteros, com lados de 8 m de comprimento.

Passo 1

Vamos calcular as forças pelo método das seções, partindo a treliça em duas e considerando uma parte dela como se fosse um corpo rígido, e então resolvendo as equações de equilíbrio para esse corpo. Temos interesse nas barras , e , então o corte que devemos fazer tem que cortar alguns desses elementos, preferencialmente. Faremos um corte passando por , e , e consideraremos o lado direito, como mostra a figura:

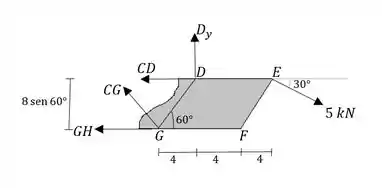
Para resolver as equações de equilíbrio nesse corpo, precisamos primeiro encontrar a força .

Passo 2

Para encontrar , igualamos a zero o momento em torno do ponto da treliça como um todo. Usamos esse ponto pra não termos na equação as forças desconhecidas de . As distâncias horizontais e verticais dos pontos até são facilmente calculadas somando os lados dos triângulos, e a força de 5 kN foi decomposta em força vertical e horizontal. Consideramos os momentos anti-horários como positivos. Então:

Isolando , encontramos o valor:

Passo 3

Agora que temos , podemos achar as forças pedidas nas equações de equilíbrio para o corpo que separamos. Primeiro vamos tentar achar . Como queremos uma equação que não contenha as outras duas forças para encontrarmos diretamente, fazemos o momento em torno de ( e passam nesse ponto).

Resolvendo a equação encontramos :

Passo 4

Para achar fazemos o somatório das forças verticais ser zero:

Isolando achamos o valor da força:

O valor negativo indica que o sentido da força mostrado no desenho está errado.

Passo 5

Agora que temos e , podemos fazer as equações de equilíbrio para o nó para tentar achar . Nesse nó só temos duas forças desconhecidas, e , então com as duas equações de equilíbrio conseguiremos achar .