Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 29
Determine as forças nos elementos e .
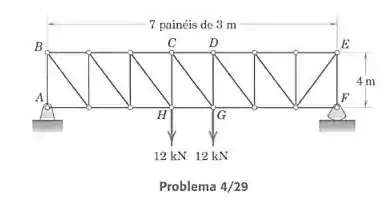
Passo 1
Vamos calcular as forças pelo método das seções. Primeiro resolvemos as equações de equilíbrio para determinar as forças externas em e e depois traçaremos uma seção vertical entre e , separando a treliça em duas. Vamos às equações de equilíbrio da treliça como um todo. Note que o apoio em gera apenas força vertical, e que pela simetria .
Passo 2
Agora vamos dividir a treliça e tratar a parte da esquerda como um corpo rígido:
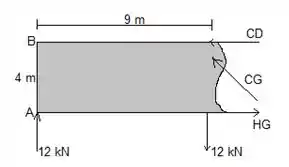
Podemos fazer a equação de equilíbrio em pra achar :
E o momento em relação a para obter :
Resposta
Exercícios de Livros Relacionados
Determine a força no elemento B E da treliça carregada.
Determine as forças nos elemento D E e D L .
Determine as forças nos elementos B C e F G da treliça simétrica carregada. Mostre que esse cálculo pode ser realizado usando uma seção e duas equações, cada uma das quais contendo apenas uma das duas
Determine a força no elemento A E da treliça carregada.
Determine a força no elemento D G da treliça carregada.