Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 49
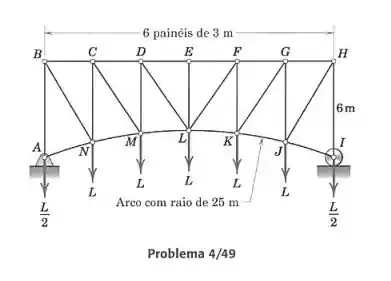
Determine a força no elemento da treliça simétrica carregada.
Passo 1
Vamos calcular as forças pelo método das seções, partindo a treliça em duas e considerando uma parte dela como se fosse um corpo rígido, e então resolvendo as equações de equilíbrio para esse corpo. Temos interesse na barra , então o corte que vamos fazer tem que passar nesse elemento. Vamos então fazer uma linha passando por , e :
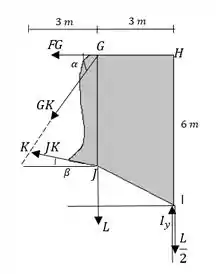
Agora temos nossa seção, devemos achar as forças através das equações de equilíbrio.
Passo 2
Temos primeiro que encontrar a força feita pelo apoio em . Pela simetria da treliça e fazendo uma equação de equilíbrio vertical da treliça como um todo, conseguimos achar essa força rapidamente:
Então só temos três forças desconhecidas. Para calcular as forças, está faltando determinar os ângulos e , que vão entrar nas contas.
Passo 3
Vamos descobrir a coordenada dos pontos , , e , sendo a origem o centro do arco de 25 m (abaixo do ponto . Para os pontos , e que estão no arco, temos:
Então:
está 6 m acima de então:
Passo 4
Agora, através das coordenadas dos pontos, conseguimos saber quem são os ângulos e . Vamos lá:
O ângulo é o ângulo entre a horizontal e :
Passo 5
Bom, agora já temos tudo o que precisamos para aplicar as equações do equilíbrio no corpo visando achar . Vamos olhar de novo nosso diagrama de corpo livre:
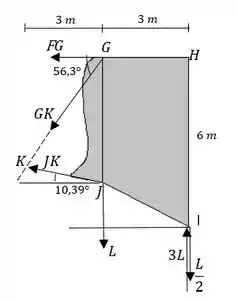
Olhando a figura, vemos que e tem a linha de ação passando por . Então se fizermos a equação de momento em torno de só aparecerá na conta de incógnita e então resolveremos diretamente. A altura de em relação a é . Então:
O sinal negativo indica que a força é de compressão, e não de tração como supomos no desenho.
Passo 6
Agora que só temos duas incógnitas, fazemos as equações de equilíbrio em e para encontrar .
Substituindo os valores dos cossenos e :
Isolamos pra substituir na próxima equação:
Agora para :
Substituimos agora pelo valor achado anteriormente, encontramos finalmente o valor de :
Como o resultado é positivo, a força é de tração, como suposto.