Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 151
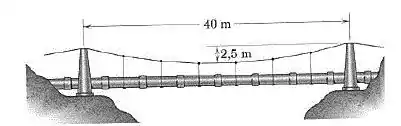
Um tubo de água horizontal de 350 mm de diâmetro é sustentado sobre uma ravina pelo cabo mostrado. O tubo e a água dentro dele têm uma massa combinada de 1400 kg por metro de seu comprimento. Calcule a força compressiva C exercida pelo cabo em cada suporte. Os ângulos feitos pelo cabo com a horizontal são os mesmo em ambos os lados de cada suporte.
Passo 1
Primeiro vamos anotar as informações que a questão e a imagem nos oferecem, para facilitar a visualização:
Agora, vamos lembrar a equação da força trativa máxima relacionada com o comprimento total:
Também, temos que:
Ou,
Outra relação importante que devemos lembrar é:
Portanto a força compressiva C é dada pela soma das forças, ou seja,
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira, temos:
Substituindo os valores, teremos:
Resolvendo,
Conhecendo a força trativa máxima, podemos substituir na equação abaixou:
Logo,
Dessa maneira, como conhecemos a equação que relaciona o ângulo com é só substituir. Como isso,
Passo 3
Agora que já conhecemos o ângulo, basta fazer a soma das forças em y, que teremos
Logo,
Com isso, a força compressiva é dada por: