Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 39
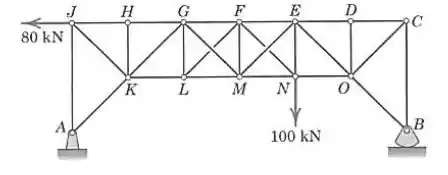
A treliça mostrada é formada por triângulos retângulos de . Os elementos cruzados nos dois painéis centrais são barras de amarração esbeltas incapazes de suportar compressão. Mantenha as duas barras que estão sob tração e calcule os módulos de suas forças trativas. Encontre também a força no elemento .
Passo 1
Vamos chamar de a distância entre os pontos que estão marcados na treliça (com exceção de e ), e então vamos considerar as forças externas que atuam sobre ela.
Além das forças de e de , temos as forças e agindo nos suportes, e as duas são desconhecidas. Se calcularmos o momento em relação a um desses pontos, vamos ficar com apenas uma variável desconhecida:
E a força em está a uma distância do pondo , a força de está a e a força de está a :
E então podemos cortar o e isolar a força :
Passo 2
Agora vamos pensar em um outro trecho da treliça (método das seções) de forma a encontrar a força , que é um dos “elementos cruzados nos dois painéis centrais”. Lembrando que o enunciado pediu para “mantermos” as barras que estão sob tração.
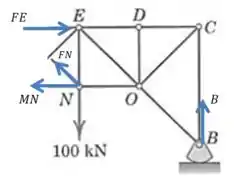
No método das seções nós tratamos o trecho da treliça como se fosse um único corpo em equilíbrio, e por isso só consideramos as forças externas. Também é importante não se preocupar muito com o sentido de cada força no desenho, o que importa é acertar a direção.
E agora vamos aplicar a condição de equilíbrio das forças na direção vertical:
E podemos aproveitar essa mesma configuração para achar a força . Vamos calcular o momento em relação ao ponto :
Nesse caso a força tem momento nulo, e então:
Passo 3
E agora vamos fazer praticamente a mesma coisa, mas com outra seção, e dessa vez queremos encontrar a força em :
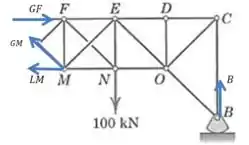
E mais uma vez vamos usar a condição de equilíbrio das forças na direção vertical:
Resposta
As forças são e . Em todos os casos as forças são de tração.